Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Ingenierías Universidad de Medellín
Print version ISSN 1692-3324
Rev. ing. univ. Medellín vol.11 no.21 Medellín July/Dec. 2012
ARTÍCULO ORIGINAL
JOB SHOP SCHEDULING BIOBJETIVO MEDIANTE ENFRIAMIENTO SIMULADO Y ENFOQUE DE PARETO
JOB-SHOP SCHEDULING: BIO-OBJECTIVE THROUGH SIMULATED COOLING AND PARETO PRINCIPLE
Juan Carlos Osorio*; Diego Fernando Lasso**; Gabriel Alonso Ruiz***
* Escuela de Ingeniería Industrial y Estadística. Universidad del Valle. Calle 13 No 100-00, Santiago de Cali, Colombia. Email: josorio@pino.univalle.edu.co. Autor de correspondenci.
** Escuela de Ingeniería Industrial y Estadística. Universidad del Valle. Santiago de Cali, Colombia. Email: diegofernandolasso@gmail.com.
*** Escuela de Ingeniería Industrial y Estadística. Universidad del Valle. Santiago de Cali, Colombia. Email: gabaloruiz@hotmail.com.
Recibido: 04/02/2011
Aceptado: 05/10/2012
RESUMEN
El problema del scheduling es uno de los problemas más ampliamente tratados en la literatura; sin embargo, es un problema complejo NP hard. Cuando, además, se involucra más de un objetivo, este problema se convierte en uno de los más complejos en el campo de la investigación de operaciones. Se presenta entonces un modelo biobjetivo para el job shop scheduling que incluye el makespan y el tiempo de flujo medio. Para resolver el modelo se ha utilizado una propuesta que incluye el uso del meta-heurístico Recocido Simulado (SA) y el enfoque de Pareto. Este modelo es evaluado en tres problemas presentados en la literatura de tamaños 6x6, 10x5 y 10x10. Los resultados del modelo se comparan con otros meta-heurísticos y se encuentra que este modelo presenta buenos resultados en los tres problemas evaluados.
PALABRAS CLAVE
Scheduling, Job shop multiobjetivo, optimización multiobjetivo, frontera de Pareto, recocido simulado.
ABSTRACT
The scheduling problem is one of the most widely treated problems in literature; however, it is an NP hard complex problem. Also, when more than one objective is involved, this problem becomes one of the most complex ones in the field of operations research. A bio-objective model is then emerged for the Job-Shop Scheduling, including makespan and mean flow time. For solving the model a proposal which includes the use of Simulated Annealing (SA) metaheuristic and Pareto Principle. This model is evaluated in three problems described in literature with the following sizes: 6x6, 10x5 and 10x10. Results of the model are compared to other metaheuristics and it has been found that this model shows good results in the three problems evaluated.
KEY WORDS
Scheduling; multi-objective Job shop; multi-objective optimization; Pareto frontier; simulated annealing.
INTRODUCCIÓN Y REVISIÓN DE LA LITERATURA
El scheduling se considera como el nivel más bajo en la planeación de la producción, y consiste en una toma de decisiones para determinar la organización de la producción considerando la disponibilidad de recursos y restricciones, ya sean físicas o por políticas de producción.
Aunque la literatura existente en torno al problema del scheduling es abundante, la mayoría de estos trabajos ha considerado solamente un criterio como función objetivo, pero la práctica demuestra que el problema involucra más de un objetivo, que en muchas oportunidades, se presentan en conflicto. Tal como lo plantean T´kindt y Billaut [1] un problema genuino de scheduling, en esencia, involucra múltiples objetivos.
Hasta finales de los 80, la mayoría de los trabajos existentes consideraban un solo criterio en su función objetivo, mientras que en la práctica, este aspecto es multidimensional, y para medir la efectividad de esta actividad en la empresa, se conjugan múltiples elementos, tales como los inventarios de trabajo en proceso, la utilización de los equipos y el cumplimiento con las fechas de entrega ofrecidas a los clientes. Ello ha obligado el desarrollo del scheduling multiobjetivo [2].
Si bien es cierto que este tema es relativamente nuevo en la literatura correspondiente al problema del scheduling, es claro que los últimos desarrollos al respecto se ven obligados a incluirlo, más cuando se aprecia que esto hace más realista la situación y permite una consideración más práctica de la problemática.
Básicamente resolver un problema de scheduling es dar respuesta a tres variables de organización de la producción que son:
• La asignación de pedidos, equipo y personal a los centros de trabajo.
• Determinar la secuencia de realización de las actividades.
• La programación de las fechas de comienzo y finalización de las operaciones.
Tal como se aprecia, estas variables pueden tener objetivos encontrados, y la solución óptima para una, muchas veces genera conflicto con las otras. Ello hace necesaria la búsqueda de una solución que satisfaga al sistema, y no a sus elementos de manera aislada.
La optimización multiobjetivo ha sido utilizada ampliamente en áreas donde un problema involucra múltiples objetivos frecuentemente en conflicto, que deben ser optimizados simultáneamente. Entre estas aplicaciones, aparece el problema del scheduling [3].
Considerando un problema con k ≥ 2) funciones objetivo a ser minimizadas simultáneamente, esta técnica busca encontrar una solución x perteneciente a un conjunto de soluciones factibles X que resuelva el problema:
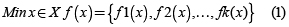
Como se asume que los objetivos están en conflicto, no hay un valor de x que minimice todos los objetivos de manera simultánea, por lo cual se requieren métodos diferentes [4]. Se define entonces un problema multiobjetivo de scheduling, al problema que consiste en calcular un programa que satisface varios objetivos en conflicto.
Entre los enfoques presentados para la solución de problemas multiobjetivo se puede mencionar el enfoque simultáneo (Pareto) cuyo propósito es generar –o aproximar en caso de utilizar métodos heurísticos– el conjunto completo de soluciones eficientes [5].
Históricamente el problema del scheduling multiobjetivo ha sido particularmente importante. En 1988, Dileepin y Sen sugirieron que la investigación tendría uno de dos enfoques: considerar un criterio como objetivo y el otro como restricción, o combinar los dos criterios en un solo objetivo [4].
En cuanto a los métodos utilizados para resolver el problema, se cuentan modelos de asignación, algoritmos de Branch and bound y la programación dinámica. Se pueden mencionar importantes revisiones sobre los avances en la temática a lo largo del tiempo. Haral, Chen, Ferrell y Kurz [4] hacen referencia a las revisiones de Fry en 1989, Nagar en 1995, Raghavachari en 1995 y el trabajo de T´kind en 2001.
Por su parte, T´kindt y Billaut [1] presentan en este libro una revisión de los métodos utilizados para resolver el problema del scheduling multicriterio, incluyendo tanto los métodos de optimización, como los heurísticos asociados propiamente al problema del scheduling. También es importante el trabajo de Hoogeveen [2] quien presenta una revisión detallada de los avances más significativos en el tema. Este trabajo incluye, además, un par de ejemplos que permiten comprender mejor la problemática; adicionalmente, en este trabajo se identifica que la mayoría de los desarrollos contempla problemas biobjetivo. Particularmente, este trabajo detalla la problemática asociada a la tardanza, el scheduling con tiempos de proceso controlados y los modelos de solución que se vienen desarrollando.
En cuanto a aplicaciones específicas, se puede comentar el trabajo de Lee, Chen y Kang [6], quienes presentan un enfoque multicriterio con elementos fuzzy para resolver el scheduling. Este modelo es resuelto con búsqueda Tabú, y se valida mediante un problema sencillo de 1 máquina y 6 trabajos con tiempos de procesamiento y fechas de entrega conocidos. Para la solución fueron considerados tres objetivos: tiempo total de flujo, tardanza máxima y mínimo número de trabajos tardíos. Para definir el peso de cada objetivo en la función de solución se utilizan aspectos lingüísticos mediante conceptos de lógica fuzzy.
De los más recientes trabajos se puede comentar el de Loukil, Teghem y Tuyttens [5], donde se plantea un modelo teórico para resolver el problema utilizando meta-heurísticos, específicamente enfriamiento simulado multiobjetivo (Multiobjective Simulated Annealing –MSA–). Para la evaluación del modelo planteado se utilizan problemas teóricos, algunos generados mediante simulación y otros tomados de la literatura existente. Este trabajo considera tres casos: el problema de una máquina, el de las máquinas paralelas y un flow shop permutado.
Los resultados logrados en la aplicación mencionada son, en muchas ocasiones, similares a los mejores resultados logrados por los autores de los artículos utilizados como referencia, y en los casos en que los resultados difieren, la distancia entre la solución presentada y la mejor obtenida es estrecha. Es importante aclarar que todos los problemas desarrollados en este trabajo son biobjetivo y se resuelven utilizando la técnica de Pareto Optimality.
En otro de los más recientes artículos, Haral, Chen, Ferrell y Kurz [4] presentan un algoritmo genético que busca entregar un ''buen'' programa (no el óptimo), para el caso del problema de una sola máquina. Lo interesante de este trabajo es que considera lo que los autores han denominado requerimientos no tradicionales, es decir, objetivos y restricciones que no se han tratado en la literatura, pero que se ubican en la práctica, asociados a los aspectos específicos de los ambientes de trabajo. Se utiliza el enfoque de Pareto y se definen dos objetivos tradicionales y uno no tradicional. Sin embargo, los problemas resueltos son biobjetivo, en los cuales combina por ejemplo dos objetivos tradicionales en algunos, y un objetivo tradicional y uno no tradicional en el otro. Los resultados obtenidos con la aplicación anterior son en general buenas soluciones. Pero lo que se debe destacar de este trabajo es la inclusión de los denominados objetivos no tradicionales, porque se aproxima más el problema a los ambientes reales de manufactura.
Precisamente, con respecto a las aplicaciones en ambientes reales, se presenta el trabajo de Chang, Hsieh y Wang [7] quienes a través de algoritmos genéticos resuelven un scheduling multiobjetivo para una industria electrónica Taiwanesa. En este problema consideran dos objetivos: minimizar el makespan y minimizar la tardanza. Además, resuelven el modelo con algoritmos genéticos multiobjetivo y algoritmos genéticos multiobjetivo con tasas variables. El resultado obtenido es comparativamente mejor que el que entrega el programa informático utilizado por la compañía.
Loukil, Teghem y Fortemps [8] en uno de los más recientes trabajos publicados presentan un desarrollo para un job shop flexible aplicado en un caso real de una empresa en Túnez. En este modelo se consideran cinco objetivos: tiempo de procesamiento medio, makespan, tardanza media, tardanza máxima y número de trabajos tardíos. Para resolver el problema utilizan el meta-heurístico de recocido simulado multiobjetivo (MOSA), considerando los cinco objetivos simultáneamente, aunque también realizaron experimentos por pares de criterios, y obtuvieron resultados similares.
Es importante destacar que se buscó un método de solución sencillo de manera que fuese atractivo para la empresa. En cuanto al problema considerado, se destaca la existencia de 50 productos diferentes, los cuales se programan por órdenes semanales que incluyen productos a fabricar en qi cantidades producidas por lotes. Este trabajo sienta bases importantes con respecto a la aplicabilidad de estos modelos en ambientes prácticos, además es de los pocos trabajos que consideran en el modelo de solución más de dos objetivos al tiempo.
Considerando también la problemática en un job shop flexible, aparece el trabajo de Gao, Sun y Gen [9] quienes proponen algoritmos genéticos híbridos para resolver el problema considerando tres objetivos: makespan, carga máxima por máquina y carga total del sistema. Estos objetivos se priorizaron de manera tal que el makespan fue considerado el más importante y la carga total como el menos importante. Esto con el fin de decidir frente a soluciones que presentaran valores similares. El modelo híbrido desarrollado incluye algoritmos genéticos y un algoritmo variable de vecindad. Se examinaron 181 problemas, todos teóricos, tomados de la literatura existente, y los resultados coincidieron para 119 de los casos evaluados; además, se obtuvieron 38 soluciones con mejores resultados que los existentes.
Rangsaritratsamee, Ferrel y Kurz [10] proponen un método para resolver un problema multiobjetivo en un job shop dinámico, considerando de manera simultánea la eficiencia y la estabilidad del sistema. Para la eficiencia, consideran una combinación del makespan y la tardanza en una sola función. Y para la estabilidad utilizan las desviaciones de los tiempos de inicio entre programas sucesivos. Para la solución utilizan algoritmos genéticos de búsqueda local y medidas de desempeño multiobjetivo. Se destaca aquí, que el resultado del método logra programas más estables; sin embargo, no hay mejoras en la eficiencia.
Otro trabajo que aborda el enfoque multiobjetivo para la solución del scheduling en un job shop utilizando algoritmos genéticos es el desarrollado por Esquivel, Ferrero y Gallard [3]. En este caso se consideran tres parámetros de desempeño: el makespan, la tardanza global y el tiempo de terminación ponderado. Estas tres funciones objetivo se agregan en una sola y mediante la técnica de Pareto logran resultados interesantes y motivan la continuidad en esta línea de investigación.
En la revisión del estado del arte se ha encontrado también una corriente que empieza a tomar fuerza en este tipo de problemas, y es la que involucra elementos asociados a la lógica fuzzy en los modelos de solución. De estos trabajos se destacan en los últimos años el de Sakawa y Kubota [11] quienes plantean un modelo multiobjetivo para un job shop scheduling considerando tiempos de procesamiento fuzzy y fechas de entrega igualmente fuzzy. Este problema lo construyen con tres objetivos derivados de la definición de un índice agregado del tiempo de terminación fuzzy con respecto a las fechas de entrega fuzzy. Los objetivos entonces son: maximizar el índice agregado, maximizar el índice agregado promedio y minimizar el máximo tiempo de terminación. Este modelo se resuelve a través de algoritmos genéticos y al comparar los resultados obtenidos mediante enfriamiento simulado, se encuentra que los resultados de este enfoque son mejores para los problema 6x6 y 10x10.
Otro enfoque con lógica difusa es planteado por Ghrayeb [12] quien desarrolla un modelo biobjetivo con elementos fuzzy en los tiempos de procesamiento buscando minimizar el makespan y la incertidumbre asociada a éste (por la consideración fuzzy). Se construye entonces una función que suma los dos objetivos y establece un peso para cada uno de ellos. La solución es generada a través de algoritmos genéticos biobjetivo.
Finalmente, se encuentra también una propuesta para resolver un job shop multiobjetivo involucrando elementos fuzzy en la definición de los niveles de prioridad de las funciones objetivo [13]. Este modelo involucra tres objetivos: minimizar el makespan, el número de trabajos tardíos y los costos totales por penalización del programa. Este modelo es evaluado en un ambiente real de manufactura para una empresa en Gran Bretaña y se resuelve utilizando algoritmos genéticos.
A continuación se presenta el modelo matemático desarrollado, el cual resuelve el problema biobjetivo a través del meta-heurístico recocido simulado (SA) y el enfoque de Pareto.
1 MODELO PROPUESTO
1.1 Configuración del job shop y definición del modelo
El modelo se implementó en un job shop que cumple las siguientes características:
• Ningún trabajo puede ser procesado más de una vez en la misma máquina.
• Cada máquina puede procesar solo una tarea a la vez.
• No hay tiempos de cambio entre trabajos ni máquinas.
• Hay solo una máquina por cada estación de trabajo.
• El release time se asume cero para todos los trabajos.
• Las máquinas están disponibles en cualquier momento.
• Dos operaciones del mismo trabajo no se pueden procesar simultáneamente.
• Ninguna operación tiene prioridad sobre las demás.
• Cada trabajo debe visitar todas las máquinas antes de completarse.
• Las operaciones no se pueden interrumpir.
• Un trabajo puede iniciarse en cualquier momento siempre y cuando la máquina esté disponible.
• Cada trabajo es procesado hasta concluirse, aunque haya que esperar y retardarse entre las operaciones procesadas.
En este modelo sobresalen dos conjuntos de restricciones a considerar por su importancia, de las cuales uno de los conjuntos tiene variables enteras binarias (de decisión) que son utilizadas para implementar las restricciones disyuntivas. El primer grupo tiene que ver con las restricciones de precedencia, donde se indica que operación se inicia antes que otra, y el segundo grupo de restricciones tiene que ver con las restricciones de no traslape (disyuntivas) y cuyo propósito es garantizar que una máquina no procesará dos operaciones a la vez. Para las restricciones de precedencia se va a denotar Cjk como el tiempo de terminación del trabajo j en la máquina k y a pjk como el tiempo de procesamiento del trabajo j en la máquina k.
Primero se va a considerar la restricción de precedencia de operaciones para una secuencia dada. Para un trabajo j, si el procesamiento en una máquina h precede al de una máquina k, se necesita seguir la siguiente restricción:

Ahora se considerara la restricción de no traslape de operaciones para una máquina dada. Para dos trabajos i y j, donde ambos necesitan ser procesados en la máquina k, si el trabajo i se procesa primero que el trabajo j necesitamos la siguiente restricción:

De otra forma si j se procesa primero que i, entonces se requiere que se cumpla la siguiente restricción:

Para el manejo de las restricciones (3) y (4), es útil definir un coeficiente indicador como sigue:
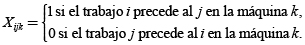
Entonces se puede reescribir las restricciones anteriores como sigue:
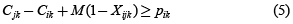
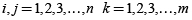
Donde M es un número positivo grande. La desigualdad anterior representa claramente la restricción de no traslape. Si el trabajo i se debe hacer primero, Xijk es uno, lo que al restarse M(1–1) es cero, obligando de esta manera al estricto cumplimiento de la restricción. De otra manera, si el trabajo j es primero, Xijk es cero, lo que al restarse M(1–0) hace que su límite izquierdo aumente, permitiendo que este crezca por encima de pik.
Para efectos de comparación se trabajaron el makespan (Cmax) y el tiempo de flujo medio (F∑) como objetivos a optimizar. De esta manera, el modelo puede ser formulado así:

Sujeto a:
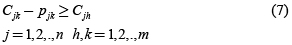
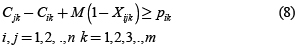
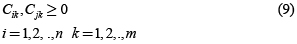

Donde la restricción (7) asegura que la secuencia de procesamiento de las operaciones de cada trabajo corresponda a la orden determinada y la restricción (8) asegura que cada máquina procese un trabajo a la vez.
1.2 Algoritmo del S. A.
Para resolver el modelo se utilizó el meta-heurístico SA con la siguiente notación:
S Solución actual
S* Mejor solución encontrada
Sn Solución generada
F(s) Valor de la función objetivo para la solución S
To Temperatura inicial
L Número de repeticiones permitida en cada nivel de temperatura
p Probabilidad de aceptar Sn cuando esta no sea mejor que S
El algoritmo básico se presenta a continuación:
Paso 0:
• Se inician los parámetros de control (To, L).
• Se define un criterio de parada.
• Se selecciona una solución inicial So.
• Se establecen los parámetros: T = To, S = So, S* = So.
• Se evalúa f(S0).
• Se establece l = 1.
Paso 1:
• Se genera una solución Sn en el vecindario de So.
• Se calcula Δ = F(Sn) – F(S).
• Si Δ ≤ 0, S = Sn y se va al paso 4.
Paso 2:
• Si Δ > 0, se calcula p = e–Δ/T.
• Se genera un número aleatorio r ∈(0,1).
• Si r ≤ p, S = Sn, y se va al paso 5.
Paso 3:
• Si r ≤ p, S = S y se va al paso 5.
Paso 4:
• Si f(S) < f(S*), S* = S.
Paso 5:
• Se hace l = l + 1.
• Si l > L se reduce la temperatura.
• Si el criterio de parada no se cumple se va al paso 1, de lo contrario el proceso se congela, y S* es la secuencia escogida.
En resumen, el algoritmo parte de una solución inicial del problema. En el ciclo interno del algoritmo, repetido mientras l < L, se genera una solución vecina Sn de la solución actual S. Si Δ ≤ 0, Sn es mejor que S, entonces la solución generada reemplaza la actual, de lo contrario la solución es aceptada teniendo en cuenta la probabilidad p = e–Δ/T calculada previamente. El valor de la temperatura T, decrece con cada iteración del algoritmo en el ciclo externo.
1.3 Generación de soluciones en un vecindario
Esto es fundamental para garantizar el éxito del algoritmo. Para este trabajo se ha utilizado la siguiente manera de generar las soluciones vecinas [14]:
Dada una permutación cualquiera de n trabajos:
1. Se generan dos números aleatorios: ai ∈ [0,n] i = 1,2.
2. Se intercambian las piezas con los valores a1, a2 en la secuencia.
1.4 Generación de la frontera de Pareto
En los puntos anteriores se ha descrito la técnica SA para la optimización de un solo objetivo, sin embargo es necesario ahora integrar la técnica con la búsqueda de la optimización multiobjetivo denominada MOSA (Multi-Objective Simulated Annealing). El objetivo de la aproximación simultánea o de Pareto es generar un conjunto de soluciones eficientes de tal forma que proporcione valores para todas las funciones objetivo aceptable para la persona que decide.
En este trabajo se propone la implementación de 3 fases para la obtención de la frontera de Pareto conformada por las soluciones no dominadas. La primera fase comprende la optimización de la función objetivo 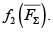
En esta primera fase, se inicia el algoritmo partiendo de la solución inicial obtenida para Cmax, es decir, que el algoritmo inicia la búsqueda en dirección al objetivo 2 partiendo de una buena solución para el objetivo 1. Esta solución es obtenida tratando de minimizar el (Cmax) para lo cual se utilizó una heurística basada en la regla LPT (Longest Processing Time). Finalmente se obtiene un conjunto de soluciones conformado por todas las soluciones aceptadas por el algoritmo en esta primera fase.
La segunda fase comprende la optimización de la función objetivo f1(Cmax). En esta fase, la solución inicial es la mejor solución obtenida para f2 por el algoritmo en la fase 1, es decir, que el algoritmo inicia la búsqueda en dirección al objetivo 1 partiendo de una buena solución para el objetivo 2. De esta manera se obtiene un conjunto de soluciones conformado por todas las soluciones aceptadas por el algoritmo en la fase 2.
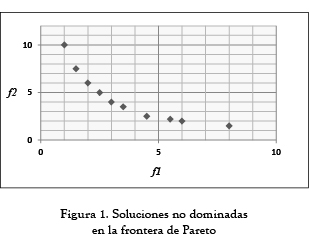
Hasta aquí se obtiene un conjunto de soluciones generadas en las 2 fases, sin embargo, es necesario seleccionar las soluciones Pareto óptimas, de esta manera se obtiene la frontera de Pareto conformada por el conjunto de soluciones no dominadas mostrado en la figura 1.
1.5 Temperatura de inicio (Ti)
La temperatura de inicio debe de ser lo suficientemente caliente para permitir un movimiento hacia cualquier lugar en el ''vecindario''. De no ser así, la solución sería la misma solución inicial o una muy cercana a esta. Pero si por el contrario la temperatura de inicio es muy alta, la búsqueda podrá moverse hacia cualquier lugar en el vecindario, convirtiéndose está en una búsqueda aleatoria. Esto deberá ser así hasta que la temperatura sea lo suficiente mente fría como para empezar a comportarse como un algoritmo SA. Aunque hasta el momento no existe ningún método para obtener la temperatura de inicio de un determinado tipo de problemas, es necesario tener en consideración otros factores.
Algunos autores han planteado métodos para obtener la temperatura inicial. Un ejemplo es Rayward y Smith [15], los cuales propone comenzar con una alta temperatura y enfriarla rápidamente hasta que un 60% de los cambios aceptados han sido soluciones más deficientes. Una vez allí, se puede continuar con un enfriamiento más lento convirtiéndose este en la temperatura de inicio.
Otro ejemplo similar es el sugerido por Dowsland [16], el cual consiste en calentar rápidamente el sistema hasta que un cierto número de soluciones más deficientes han sido aceptadas, para después comenzar con un enfriamiento lento. Serap y Kurt [17] concluyen, por su parte, que el valor de la temperatura inicial debe permitir que el valor de la probabilidad de aceptación sea 0.99 y plantean la siguiente ecuación para hallar este valor de Ti:

Donde fmin y fmax son los límites inferior y superior respectivamente para un programa dado. Otros investigadores como Babak y otros [18] plantean que la temperatura inicial para la primera iteración del algoritmo, debe permitir que la probabilidad de aceptar una solución peor sea por lo menos del 80%. Rajendran, [19] por su parte, concluye que esta debe permitir que una solución peor en un 30% de la solución inicial, se acepte con una probabilidad del 95% en la primera iteración.
1.6 Temperatura final (Tf)
Es común encontrar que la temperatura disminuya hasta que esta es cero, pero esto haría que el algoritmo corriera por un tiempo muy largo. En la práctica esto es totalmente innecesario, ya que a medida de que la temperatura se aproxima a cero, la probabilidad de aceptar un resultado menos favorable tiende a cero también. Es por esto que el criterio de parada suele ser muy baja temperatura o cuando los movimientos hechos no están generando ni mejores ni peores resultados.
Para este trabajo se calculó el valor de la temperatura de finalización de acuerdo con la siguiente ecuación [17]:

Donde 0.002 ≤ Δ ≤ 0.005.
1.7 Decrementos de temperatura
Una vez se tienen las temperaturas de inicio y finalización se necesita llegar de la una a la otra mediante decrementos de temperatura, este factor es crítico para el éxito del algoritmo. En teoría se debe permitir suficientes iteraciones de tal manera que el sistema no se enfríe muy rápido. Una manera de disminuir la temperatura es usando una ecuación lineal [16]:

Donde α < 1 y constante.
Muchos autores [18] han mostrado que α debería de estar entre 0.7 y 0.95, y que los mejores resultados se hallarán en los valores grandes de este. Claro que entre más grande sea el α, mayor será el tiempo en decrecer la temperatura y alcanzar el criterio de parada.
1.8 Iteraciones en cada temperatura
La última decisión a tomar es cuantas iteraciones deberán hacerse en cada temperatura. Aunque un número constante parece ser la respuesta obvia, en este trabajo se sugiere realizar solo una iteración por temperatura pero disminuir la temperatura rápidamente en las primeras iteraciones y muy lentamente en las siguientes [19]. La fórmula usada es:

Donde β es un número muy pequeño.
Este enfriamiento rápido tiene la ventaja de que la probabilidad de aceptar peores movimientos es más pequeña al incrementar el número de iteraciones de búsqueda.
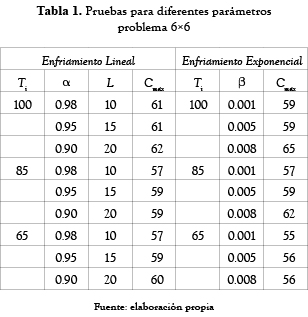
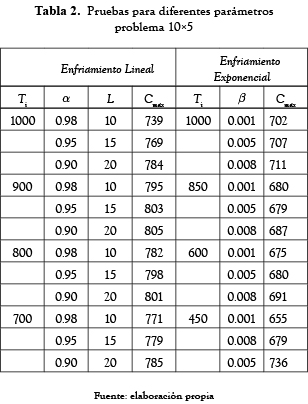
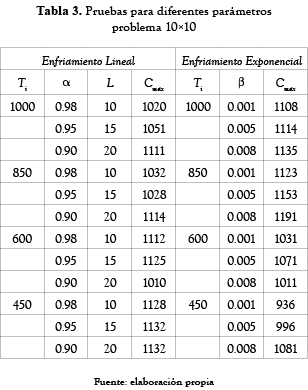
Los resultados obtenidos se muestran en las tablas 1, 2 y 3. Se observó que al usar una ecuación exponencial se obtienen mejores resultados y estos se logran cuando β es igual a 0.001.
1.9 Pruebas realizadas
Antes de resolver los problemas planteados, se observó el comportamiento de la función objetivo para diferentes valores de Ti, α, L para el caso del enfriamiento lineal y Ti y β para el exponencial. Los resultados de estas pruebas se presentan en las tablas 1, 2 y 3.
Después de realizar varias ejecuciones para diferentes parámetros se observó que los mejores resultados para los problemas tratados, se obtienen cuando en la primera iteración la probabilidad de aceptar una solución un 30% peor, es de un 70%. Aunque esta condición establece una temperatura de inicio más baja que las mencionadas anteriormente, las pruebas realizadas muestran que con este valor, se logra aceptar soluciones hasta un 250% peor que la temperatura de inicio, asegurando de esta manera un recorrido amplio sobre el espacio de soluciones.
2. RESULTADOS Y ANÁLISIS
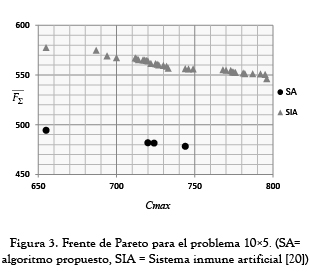
Con el propósito de validar el modelo propuesto se realizaron dos tipos de comparaciones: la primera con los resultados obtenidos por [20], quien desarrolló un Sistema Inmune Artificial (SIA) para resolver una gran cantidad de problemas job shop desde la perspectiva bi-objetivo con la optimización del Cmax y F∑. Aunque en su investigación solo presenta la frontera generada para el problema 10x5, se realizó la comparación para tener una referencia del comportamiento del modelo propuesto por lo menos en este problema.
La segunda comparación se realizó con las diferentes técnicas de solución encontradas en la literatura que presentan resultados para los problemas planteados desde la perspectiva mono-objetivo con la optimización del Cmax con el interés de conocer qué tan bueno fue el resultado del SA por lo menos para este objetivo [20].
2.1 Resultados multi-objetivo
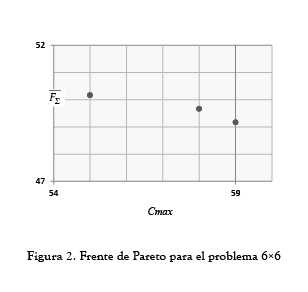
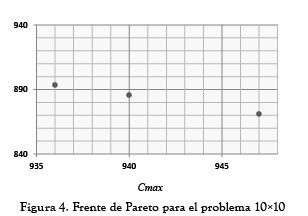
Las figuras 2, 3 y 4 muestran la frontera de Pareto obtenida después de implementar la tercera fase a las soluciones aceptadas por el SA y se compara con la frontera Pareto hallada por [20] mediante el SIA (como se explicó anteriormente solo para el problema 10x5, ya que para los demás problemas el autor concluye que solo se obtuvo un punto). Como se puede observar en los problemas 6x6 y 10x10 el SA pudo encontrar más de un punto en la frontera de Pareto mostrando ser efectivo como herramienta multiobjetivo. Sin embargo, en el problema de tamaño 10x5 aunque se encontraron menos puntos comparados con los hallados por [20], las soluciones fueron considerablemente mejores respecto al F∑. Con un Cmax igual en ambos casos (655) se obtuvo un F∑ de 494.3 el cual fue 16.85% mejor que el encontrado usando el SIA.
2.2 Resultados mono-objetivo
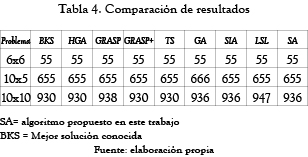
Tal como se presenta en [20], el algoritmo propuesto se compara con algunos otros métodos existentes en la literatura con respecto al mejor resultado obtenido del Cmax para los problemas planteados en este trabajo. En la tabla 4 se puede observar que para el problema de tamaño 6x6 todos los algoritmos llegaron al valor de la mejor solución conocida. En el problema de tamaño 10x5 se puede observar que el SA alcanzó el mejor resultado conocido y muestra una mejora respecto al resultado obtenido por GA. De la misma manera el SA muestra una mejora importante frente a los algoritmos GRASP, GA y LSL en el problema de tamaño 10x5; sin embargo, se observa que frente a los algoritmos HGA, GRASP+ y TS tiene una significativa desventaja.
3. CONCLUSIONES
El algoritmo propuesto es el resultado de muchas pruebas realizadas con diferentes mecanismos basados en el principio de Recocido Simulado. En general, el algoritmo tiene un buen desempeñó en comparación con otros algoritmos que tratan de resolver el JSSP (Job Shop Scheduling Problem).
En la elaboración de este trabajo se probaron varios pares de objetivos propuestos en la literatura para problemas multi-objetivo (F∑ vs. Tmax, Tmax vs. T∑ y NT vs. Tmax); sin embargo, al usar estos objetivos en los problemas desarrollados, los resultados no mostraron un comportamiento contrario entre estos, es decir, que solo se halló un punto en la frontera de Pareto, esto debido muy probablemente a la combinación de los parámetros del problema como los tiempos de proceso de las operaciones y las fechas de entrega de los trabajos. Al experimentar con la T∑ vs. E∑ se observó un comportamiento contrario, pero desde el punto de vista práctico para los problemas planteados, minimizar E∑ representa obtener programas con un gran porcentaje de tiempo ocioso.
Una de las ventajas del algoritmo propuesto es que es muy fácil de comprender y de implementar debido a que su principio es muy sencillo. Sin embargo, la complejidad radica en el cálculo de sus parámetros ya que no existe un estándar comprobado para estos.
En este trabajo se implementó un esquema de reducción de temperatura diferente al usado en el modelo clásico del SA. Este enfriamiento exponencial, diferente del lineal que se usa tradicionalmente, mostró mejores resultados en los problemas trabajados permitiendo concluir que es mejor dedicar más tiempo a explorar en bajas temperaturas.
Después de ensayar con diversos valores para β, se llegó a la conclusión que con valores de β = 0.001 se logra obtener los mejores resultados, es decir, que es importante alcanzar un equilibrio entre el tiempo de ejecución del método dependiendo del valor asignado a los diferentes parámetros y la calidad de los resultados.
En los resultados de los ensayos realizados se pudo observar que en muchas de las iteraciones se repite algún resultado generado en iteraciones anteriores, ya que el algoritmo no tiene un mecanismo de ''memoria'', lo que aumenta el tiempo de ejecución y el tiempo necesario para alcanzar la mejor solución.
Como parte del trabajo futuro posible, se podrían estudiar planteamientos multiobjetivo distintos del JSSP, buscando lograr un conflicto entre las funciones objetivo o generar instancias donde se logre un comportamiento contrario entre al menos dos objetivos.
En lo correspondiente al SA, sería interesante determinar si existe una relación entre la solución inicial y el resultado final del algoritmo o con el tiempo que tarda en encontrar la mejor solución, para poder plantear estrategias en la construcción de la solución inicial.
Además, sería interesante estudiar el uso de otros mecanismos más elaborados de búsqueda local, tratando de buscar una generación de vecinos con ''memoria'' para no aplicar una solución más de una vez obteniendo el mismo resultado.
REFERENCIAS
[1] V. T'kindt, J.C. Billaut. ''Multicriteria Scheduling. Theory, models and algorithms'', Segunda edición. Berlín, Alemania, Springer, 2006, 359 p. [ Links ]
[2] H. Hoogeveen. ''Multicriteria scheduling'', European Journal of operational research, Vol. 167, No 3, pp. 592-623, 2005. [ Links ]
[3] S. Esquivel, S. Ferrero, R. Gallard, C. Salto, H. Alfonso, M. Shutz. ''Enhanced evolutionary algorithms for single and multiobjective optimization in the job shop scheduling problem'', Knowledge-Based Systems, Vol. 15, No 1-2, pp. 13-25, 2002. [ Links ]
[4] U. Haral, R. Chen, W.G. Ferrell Jr, M.B. Kurz. ''Multiobjetive single machine scheduling with nontraditional requirements'', International Journal of production economics, Vol. 106, No 2, pp. 574-584, 2007. [ Links ]
[5] T. Loukil T, J. Teghem, D. Tuyttens. ''Solving multi-objective production scheduling problems using metaheuristics'', European journal of operational research, Vol. 161, No 1, pp. 42-61, 2005. [ Links ]
[6] H.T. Lee, S.H. Chen, H.Y. Kang. ''Multicriteria scheduling using fuzzy theory and tabu search'', International journal of production research, Vol. 40 No 5, pp. 1221-1234, 2002. [ Links ]
[7] P. Chang, J. Hsieh, C. Wang. ''Adaptative multi-objective genetic algorithms for scheduling of drilling operation in printed circuit board industry'', Applied soft computing, Vol. 7, No 3, pp. 800- 806, 2007. [ Links ]
[8] T. Loukil, J. Teghem, P. Fortemps. ''A multiobjective production scheduling case study solved by simulated annealing'', European journal of operational research, Vol. 179, No 3, pp. 709-722, 2007. [ Links ]
[9] J. Gao, L. Sun, M. Gen. ''A hybrid genetic and variable neighborhood descent algorithm for flexible job shop scheduling problems'', Computers and operations research, Vol. 35, No 9, pp. 2892- 2907, 2008. [ Links ]
[10] R. Rangsaritratsamee, W.G. Ferrel Jr., M.B. Kurz. ''Dynamic rescheduling that simultaneously considers efficiency and stability'', Computers and industrial engineering, Vol. 46, No 1, pp. 1-15, 2004. [ Links ]
[11] M. Sakawa, R. Kubota. ''Fuzzy programming for multiobjective job shop scheduling with fuzzy processing time and fuzzy due date through genetic algorithms'', European Journal of operational research, Vol. 120, No 2, pp. 393-407, 2000. [ Links ]
[12] O.A. Ghrayeb. ''A bi-criteria optimization: minimizing the integral value and spread of the fuzzy makespan of job shop scheduling problems'', Applied soft computing, Vol. 2, No 3, pp. 197-210, 2003. [ Links ]
[13] D. Petrovic, A. Duenas, S. Petrovic. ''Decision support tool for multi-objective job shop scheduling problems with linguistically quantified decision functions'', Decision support systems, Vol. 43, No 4, pp. 1577-1538, 2007. [ Links ]
[14] D. F Lasso y J.C. Osorio. Un enfoque de recocido simulado para el job shop scheduling, Working paper, Universidad del Valle, 2010 [ Links ]
[15] V.J. Rayward-Smith, I.H. Osman, C.R. Reeves and G.D. Smith, ''Modern Heuristic Search Methods'', New York: John Wiley & Sons, 1996, 294 p. [ Links ]
[16] K. Dowsland and B. Díaz, ''Heuristic design and fundamentals of the Simulated Annealing,'' Revista Iberoamericana de Inteligencia Artificial, vol. 7, no.19, pp. 93-102, 2003. [ Links ]
[17] S.U. Seckiner and M. Kurt, ''A simulated annealing approach to the solution of job rotation scheduling problems,'' Applied Mathematics and Computation, vol. 188, no. 1, pp. 31-45, 2007. [ Links ]
[18] B. Abbasi, S. Shadrokh and J. Arkat, ''Bi-objective resource-constrained project scheduling with robustness and makespan criteria,'' Applied Mathematics and Computation, vol. 180, no. 1, pp. 146-152, 2006. [ Links ]
[19] T.K. Varadharajan, Ch. Rajendran. A multi-objective simulated-annealing algorithm for scheduling in flowshops to minimize the makespan and total flowtime of jobs, European Journal of Operational Research, Vol. 167, No. 3, pp. 772- 795, 2005. [ Links ]
[20] D. Cortes. ''Un Sistema Inmune Artificial para resolver el problema del Job Shop Scheduling''. Tesis para optar al grado de maestro en ciencias. Centro de investigación y estudios avanzados del instituto politécnico nacional, México D.F., México. 2004. [ Links ]