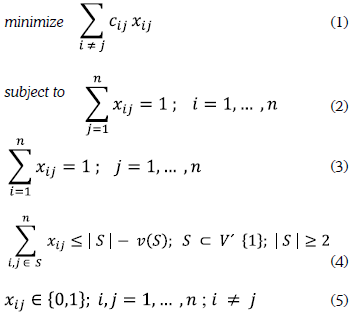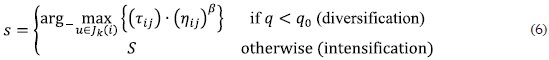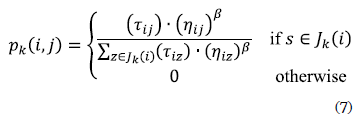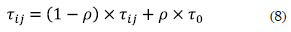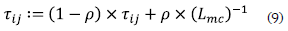Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista EIA
Print version ISSN 1794-1237On-line version ISSN 2463-0950
Rev.EIA.Esc.Ing.Antioq no.17 Envigado Jan./June 2012
SOLVING OF SCHOOL BUS ROUTING PROBLEM BY ANT COLONY OPTIMIZATION
RESOLUCIÓN DEL PROBLEMA DE RUTEO DE BUSES ESCOLARES CON OPTIMIZACIÓN POR COLONIA DE HORMIGAS
RESOLUÇÃO DO PROBLEMA DE RUTEO DE ÔNIBUS ESCOLARES COM OTIMIZAÇÃO POR COLÔNIA DE FORMIGAS
Juan S. Arias-Rojas*, José Fernando Jiménez**, Jairo R. Montoya-Torres***
*Ingeniero Industrial, Pontificia Universidad Javeriana. Order Management Team Leader - MCA and Mexico, Hewlett Packard Colombia Ltda. Bogotá, Colombia. juan.arias@javeriana.edu.co.
**Ingeniero Industrial, Pontificia Universidad Javeriana; MSc en Investigación de Operaciones, Universidad de Edimburgo, Escocia. Profesor de tiempo completo, Departamento de Ingeniería Industrial, Pontificia Universidad Javeriana. Bogotá, Colombia. j-jimenez@javeriana.edu.co.
***Ingeniero Industrial, Universidad del Norte, Barranquilla; MSc en Ingeniería Industrial y Management, Institut National Polytechnique de Grenoble, Francia y Doctor, École Nationale Supérieure des Mines de Saint-Étienne, Francia. Profesor Asociado, Escuela Internacional de Ciencias Económicas y Administrativas, Universidad de La Sabana, Bogotá, Colombia. jairo.montoya@unisabana.edu.co.
Artículo recibido 21-IX-2011. Aprobado 16-VI-2012
Discusión abierta hasta diciembre de 2012
ABSTRACT
The school bus routing problem (SBRP) seeks to plan an efficient schedule of a fleet of school buses that must pick up students from various bus stops and deliver them by satisfying various constraints: maximum capacity of the bus, maximum riding time of students, time window to arrive to school. In this paper, we consider a case study of SBRP for a school in Bogotá, Colombia. The problem is solved using ant colony optimization (ACO). Computational experiments are performed using real data. Results lead to increased bus utilization and reduction in transportation times with on-time delivery to the school. The proposed decision-aid tool has shown its usefulness for actual decision-making at the school: it outperforms current routing by reducing the total distance traveled by
8.3 % and 21.4 % respectively in the morning and in the afternoon.
KEY WORDS: school bus; routing; ant colony; case study.
RESUMEN
El problema de ruteo de buses escolares (SBRP) busca encontrar el programa más eficiente para una flota de buses escolares que deben recoger y despachar estudiantes en varias paradas de bus satisfaciendo varias restricciones: capacidad máxima del bus, máximo tiempo de recorrido de los estudiantes, ventanas de tiempo para la llegada al colegio. En este artículo se considera un caso de estudio de un problema SBRP para un colegio en Bogotá, Colombia. El problema se resuelve usando la metaheurística de colonia de hormigas (ACO). Los experimentos computacionales se realizan empleando datos reales. Los resultados muestran el incremento en el nivel de utilización de los buses y una reducción en los tiempos de transporte con despacho a tiempo en el colegio. La herramienta ha mostrado su utilidad para la planeación regular de buses en el colegio: se redujo la distancia total recorrida en 8,3 % en la mañana y en 21,4 % en la tarde.
PALABRAS CLAVE: buses escolares; ruteo; colonia de hormigas; estudio de caso.
RESUMO
O problema de roteamento de ônibus escolares (SBRP) busca encontrar o programa mais eficiente para uma frota de ônibus escolares que devem recolher e despachar estudantes em várias paradas de ônibus satisfazendo várias restrições: capacidade máxima do ônibus, máximo tempo de percurso dos estudantes, janelas de tempo para a chegada ao colégio. Em este artigo considera-se um caso de estudo de um problema SBRP para um colégio em Bogotá, Colômbia. O problema resolve-se usando a meta-heurística de colônia de formigas (ACO). Os experimentos computacionais realizam-se empregando dados reais. Os resultados mostram o incremento no nível de utilização dos ônibus e uma redução nos tempos de transporte com despacho a tempo no colégio. A ferramenta tem mostrado sua utilidade para o planejamento regular de ônibus no colégio: reduziu-se a distância total percorrida em 8,3 % na manhã e em 21,4 % na tarde.
PALAVRAS-CÓDIGO: ônibus escolares; roteamento; colônia de formigas; estudo de caso.
1. INTRODUCTION
The school bus routing problem (SBRP) has been widely studied since it was proposed in literature by Newton and Thomas (1969). As presented by Park and Kim (2010), the general SBRP seeks to plan an efficient schedule for a fleet of school buses where each bus picks up students from various bus stops and then delivers them to the school. Various constraints must be satisfied: maximum capacity of buses, maximum riding time of a student in a bus, and delivery time or time window to the school. According to the classification proposed by Desrosier et al. (1981), the SBRP consists of smaller sub-problems: data preparation, bus stop selection (student assignment to stops), bus route generation, school bell time adjustment, and route scheduling. As described in Park and Kim (2010), in the data preparation step, the road network consisting of home, school, bus depot, and the origin-destination (OD) matrix among them are specified. For a given network, the bus stop selection step determines the location of stops, and the students are assigned to them. Thereafter, the bus routes for a single school are generated in the bus route generation step. The school bell time adjustment and route scheduling steps are necessary for the multi-school configuration when the school bus system is operated by the regional board of education and not by individual schools. The reader can refer to the survey of Park and Kim (2010) for a detailed study of solution approaches for each of these SBRP steps. In most existing approaches in literature, those steps are considered separately and sequentially, although they are highly interrelated. Note that best solutions require an integrated approach. Due to the problem size and complexity, single sub-problems or a combination of them are solved as variants of existing combinatorial optimization problems. For example, the bus route generation sub-problem is very similar to the vehicle routing problem (VRP) for the general case of various vehicles (if each vehicle is considered separately, the problem becomes the well-known traveling salesman problem (TSP)), while the combined problem of bus stop selection and bus route generation falls into the class of location-routing problems (LRP) in which the vehicle routing problem (VRP) is a class of problems that fits here.
In the literature, transportation problems involving transportation of students to schools have already been studied. As the first papers published on school bus routing we can cite the works proposed by Newton and Thomas (1969), Angel et al. (1972), Bennett and Gazis (1972), Bodin and Berman (1979). More recent works on school bus routing are due to Li and Fu (2002), Spada, Bierlaire and Liebling (2005), Fügenschuh (2009), Martínez and Viegas (2011), Riera-Ledesma and Salazar-González (2012), among others. The reader is referred to the work of Park and Kim (2010) which is an updated state- of- the- art survey on different approaches to solve the school bus routing and scheduling problem. According to Braca et al. (1997), the school bus routing problem is a special case of the vehicle routing problem (VRP). In a VRP, a set of n clients (the students) has to be serviced by a fleet of vehicles (the buses). Since the buses have limited capacity, the problem becomes the capacitated vehicle routing problem (CVRP), which is known to be NP-hard.
In this paper, we consider a case study of school bus routing problem for a well-recognized school located in Bogotá, Colombia. Because of the NP-hardness of the school bus routing problem (Fügenschuh, 2009), the problem is solved using ant colony optimization (ACO) algorithm and the computational implementation is performed using real data from the school. The aim is to increase bus utilization and to reduce transportation times for students, while maintaining on-time delivery of students to the school. The reader must note that ant colony optimization has not yet been used, to the best of our knowledge, to solve the school bus routing problem. We have chosen the use of ACO algorithm because it has been shown in literature that it is one of the most studied meta-heuristic algorithms for VRP, see for example the works of Tan et al. (2005), Doerner et al. (2006), Favaretto, Moretti and Pellegrini (2007), Gajpal and Abad (2009), De la Cruz et al. (2011), among others. Hence, we use the good results obtained by the application of ACO for other vehicle routing problems and adapt the approach to solve the problem under study in this paper.
The remainder of this paper is organized as follows. Section 2 presents in detail the problem under study, while section 3 presents the proposed ACO-based algorithm to solve it. Section 4 is devoted to the computation implementation. Finally, section 5 presents some concluding remarks.
2. PROBLEM DESCRIPTION: PRESENTATION OF THE CASE STUDY AND MATHEMATICAL FORMULATION
The bus scheduling problem studied here is taken from a real-life application. The school under study is a private school located in city of Bogotá, the capital of Colombia, and founded in 1934. According to the Colombian educational system, it offers instruction at preschool, primary, secondary and medium educational levels to about 1540 students. The transportation service to students at both the beginning and the end of the school day is carried out by the school's own fleet of 11 buses. From the total of students in the school, only about 540 require transportation. Every day, buses perform two journeys. In the morning, they pick up the students at their homes, while in the afternoon the buses transport the students from the school to their houses. The reader must note that the number of students to be transported in the morning and in the afternoon is not necessary the same since some students may be either driven by their parents in the morning or picked up in the afternoon by them. Also note that several students might also be picked up or delivered at the same point (building) and hence the number of stops may be different from the number of students for a given bus. Since buses belong to the school, it is necessary that the administration office performs efficient processes for solving both the problem of student assignment to buses and then the corresponding bus routing problem to student pickup.
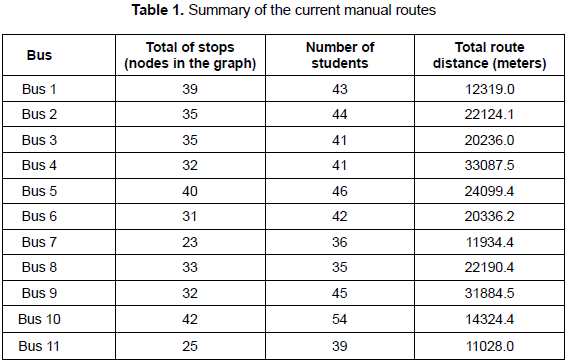
Bogotá is a very big city with about 8 millions of inhabitants. The traffic is very dense in the morning and in the afternoon corresponding to the times in which students enter and exit the school: classes start at 6:45 a.m. and finish at 3:00 p.m. Hence, one of the criteria to take into account when solving the school bus routing problem is that the time spent by students on the bus must be as lower as possible. Under these conditions, the objective of the route planner might be to minimize the total travel time of each bus. Additional constraints to this problem are the total capacity of buses (maximum of 54 students) and the limited number of buses available to perform the service. The travel speed within the city that is limited to 40 km/h for school buses is also a condition for the particular case study. Table 1 presents the details of the current manual solution for each bus for the morning route: length of routes, number of stops, and the number of students picked up.
Formally, the problem can be represented by a graph G=(V,E) where V is the set of nodes and E is the set of arcs in the graph. Each node represents a point in which students (customers in the classical VRP) have to be serviced, while an arc corresponds to the route to go from node i to node j. The weight cij of each arc represents the distance, cost or time of the route. The total number of nodes in the graph represents the total number of stops that a bus has to service, while the demand, noted as pi, of each node corresponds to the number of students to be picked up (or dropped off in the afternoon route) by the bus. The capacity of each vehicle k={1,2,..,M} is noted as Kk. It is to note that each bus starts and finishes the route at the school, which represents the depot of the routing problem. A mathematical model of the classical VRP, taken from Laporte (1992), is presented next. Let the Xij (i ≠ j) be a binary variable equal to 1 if and only if arc (i, j) appears in the optimal solution and 0 otherwise. The parameter Cij is the associated distance (or sometimes associated cost) incurred if the arc (i, j) is used. The VRP can be formulated as a modified assignment problem; it is formulated as follows:
In this formulation, equations (1), (2), (3) and (5) define a modified assignment problem (i.e. assignments on the main diagonal are prohibited). Constraints (4) allows the solution not to have unconnected cycles. As already mentioned, because the problem is known to be NP-hard, we present the use of ant colony optimization (ACO) meta-heuristic to solve it. We have chosen this meta-heuristic since it has shown to be one of the most efficient for solving complex vehicle routing problems (De la Cruz et al., 2011).
3. PROPOSED ANT COLONY ALGORITHM
Among the meta-heuristics for solving network- based routing problems, procedures based on artificial ants have been employed with a great success. Ant-based methods were inspired by the observation of real ants, particularly, the way ants can find shortest paths between food sources and their nest through a simple system of indirect low-level communication system, namely pheromone trails. This characteristic may be easily extended to artificial ants (agents) to solve hard combinatorial optimization problems, such as that of vehicle routing. Ant algorithms are seen as multiple agent procedures for solving difficult combinatorial optimization problems.
The ant colony system (ACS) algorithm (Dorigo and Gambardella, 1997) was developed to find good solutions within a reasonable computational time for routing problems. Generally, ACS procedures place a number of artificial ants (or agents) that are positioned on a set of customers (demand points) chosen according to some initialization rule. Each ant (agent) builds a feasible solution to the problem by iteratively applying a state transition rule that integrates information on what decisions are better in the short term (through a heuristic or greedy rule) and which ones are better in the long term (given by the knowledge stored in the pheromone trail). To build a solution, each agent updates a pheromone trail leading other ants to build their own solutions. Thus, the ACS algorithm guides the ants to find good solutions in a relatively short time. The reader interested in an updated taxonomy of ACO algorithms can refer to the work of Pedemonte et al. (2011).
In order to solve the problem, we implemented a strategy based on "cluster-first route-second", which has been employed in several works to solve routing problems, e.g., Dulac, Ferland and Forgues, 1980; Chapleau, Ferland and Rousseau, 1985; Bowerman, Hall and Calamai, 1995. Generally speaking, the approach consists in grouping the students into clusters so that each cluster can be served as a route satisfying the constraints that exist. In fact, for the case under study here, the problem is decomposed into two sub-problems. In the first instance, nodes of the graph (bus stops) are grouped and assigned to the buses (clustering phase). Then, each cluster is solved as a traveling salesman problem (TSP). During the assignment phase, clusters must satisfy buses capacity constraints, as well as fleet size (e.g. the number of clusters cannot exceed the number of available buses). During the second phase, each pickup (or delivery) point cannot be visited more than once. The key feature of this two-phase procedure is to define the clusters in such a way that the distance to be traveled by each bus between pickup (or delivery) points is the shorter as possible. Hence, the probabilistic nature of ACO method will very quickly find good routing. Following is the description of both phases of the solution procedure: node assignment (clustering) and routing.
3.1 Assignment
This sub-problem was solved using a heuristic method. The method starts by ordering the pickup (morning routes) and delivery (afternoon routes) points according to their geographical location in the city: from north to south and then from west to east. The assignment was hence done by consecutively selecting the stops and respecting the constraints of bus capacity and that each node can be visited by only one bus. An additional constraint was added to this procedure: to the best of the possibilities, buses are not allowed to ride on principal avenues since they are highly susceptible to traffic jams and can only be passed by specific points in the city, which will lead to a long travel distance between two points. The reader may notice that predefining the clusters might leave the optimal solution out of reach. However, the approach presented here makes sense because of the size of the problem.
3.2 Routing with the ACO algorithm
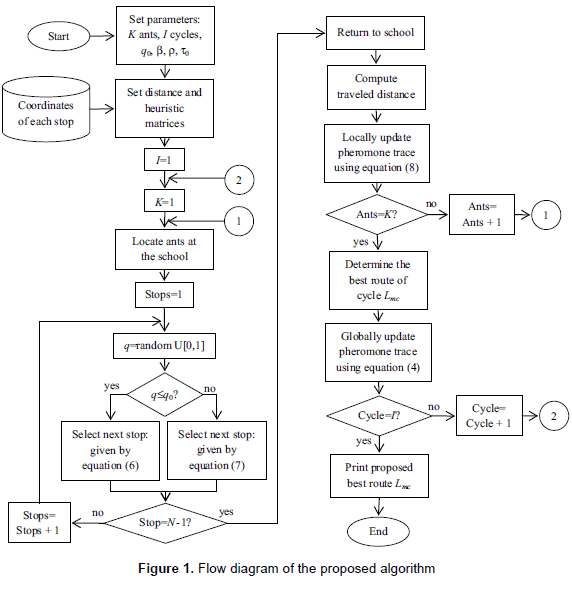
The routing phase of the procedure was solved using ant colony algorithm. This method emulates the behavior of real ants and the characteristics of their pheromone trail (update and evaporation) to find the best sequence in which buses must visit all pickup and delivery points of students. The solution must guarantee that all stops are visited only once by a bus. Figure 1 presents the flow diagram of the algorithm. For the given set of nodes V= {v1,..., vn} defined as the subset of N stops assigned to a bus and E = {(i, j): i, j  V} the set of arcs between each pair of nodes. Let dij be the distance associated to each arc (i, j). Let K be the number of ants of each cycle and I be the number of cycles executed by the algorithm. We need the heuristic matrix of size N×N where each ηij=1/dij corresponds to the desirability level of going from node i to node j. The pheromone matrix of size N×N with each τij corresponds to the level of pheromone trace present in arc (i, j). The values of the heuristic matrix are constants while those of the pheromone matrix are updated during the solution construction process. Their initial value τij = τ0 is given.
V} the set of arcs between each pair of nodes. Let dij be the distance associated to each arc (i, j). Let K be the number of ants of each cycle and I be the number of cycles executed by the algorithm. We need the heuristic matrix of size N×N where each ηij=1/dij corresponds to the desirability level of going from node i to node j. The pheromone matrix of size N×N with each τij corresponds to the level of pheromone trace present in arc (i, j). The values of the heuristic matrix are constants while those of the pheromone matrix are updated during the solution construction process. Their initial value τij = τ0 is given.
Each ant starts at the school and must travel all the stops in V to finally return to school at the end of the route. The ant builds the route using a probabilistic decision function, step by step, according to equations (6) and (7):
Where q is a random value taken from a uniform distribution between 0 and 1, and q0 (0≤q0≤1) is a given parameter. The term "diversification" refers to the choice of the ant to explore routes that have not yet been considered or explored, while the term "intensification" refers to the fact that the ant intensifies the search of a solution on routes that have high levels of pheromone. Jk(i) refers to the set of stops where ant k can go when it is at stop i (e.g. the stops that have not yet been visited). The parameter β determines the relative importance of the heuristic function related to the pheromone trail at the instance of decision making. The value of S is defined by the probabilistic function given by equation (7):
At each stop, the ant chooses its next move by computing the previous equations. Once the ant arrives to the last node, it returns to the school, computes the total travel distance and locally update the pheromones using equation (8):
When all the ants of the cycle have finished the routing, the shortest one is selected and the global pheromone trail is updated using equation (9):
where Lmc corresponds to the best route of the cycle (iteration).
Equations (8) and (9) update the trace of the pheromone matrix by both adding pheromone to traveled routes and evaporating pheromone to other routes. The value of ρ corresponds to the pheromone evaporation coefficient. This process is repeated on every cycle (iteration) of the algorithm. At the end of the last iteration, the shortest route is selected among the set of Lmc routes of each iteration (cycle). This will be the final solution given by the algorithm.
4. COMPUTATIONAL IMPLEMENTATION
4.1 Input data and parameters
Computational experiments were carried out in order to validate the proposed solution procedure of the school bus routing problem. Real data provided by the school was employed in our experiments. The classes at the school start at 6:45 a.m. and finish at 3:00 p.m. The capacity of each bus was fixed to be a maximum of 54 students. A fleet of 11 buses is available every day to perform students pick up in the morning and delivery in the afternoon. Location of pickup points (delivery points in the afternoon) is provided by the routing planner at the school. A total of 466 students located in 367 points have to be serviced in the morning, while in the afternoon 521 students have to be delivered at 398 points in the city. Shortest travel time/distance between each pair of points in the network was computed using the "Manhattan distance" method, which leads to an asymmetric matrix of distances (e.g. the distance to go from point i to point j is different from the distance to go from point j to point i).
In order to define the parameters of the ACO algorithm, we first tested those proposed by Dorigo and Gambardella (1996) for asymmetric traveling salesman problems (TSP). Preliminary runs were carried out to validate those values. As proposed by those authors, the values of parameters are: number of cycles=50×(number of stops), number of ants is 200, q0=0.9, β=5 and ρ=0.1.
4.2 Results
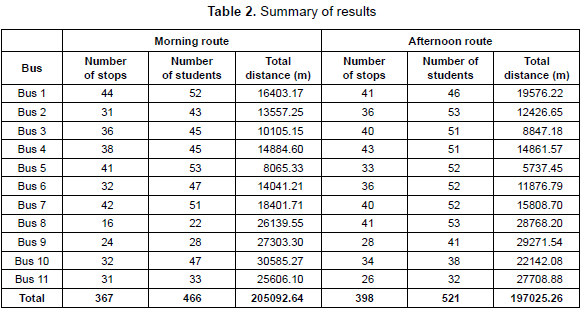
In order to define the proposed routes (for the morning and for the afternoon), the algorithm was run 10 times for each one the 11 groups of each bus. The best route was selected. Table 2 presents a summary of the proposed solutions regarding the number of stops visited by each bus, the number of students to pickup (in the morning) and to drop off (in the afternoon), as well as the total distance of the journey of each bus. In comparison with the current routing (presented previously in table 1), the proposed solution outperforms the current routing by reducing the total distance traveled by 8.3 % and 21.4 % respectively in the morning and in the afternoon. The average distance reduction is 15.2 %. This means an average reduction of a total of 5.59 hours in the morning and 5.19 hours in the afternoon for all the buses: that is the total route is being reduced by near to 30 minutes in average for each bus.
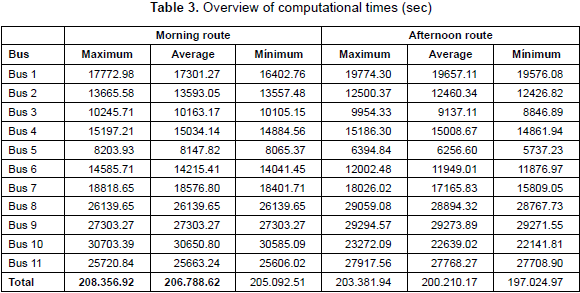
Concerning computational times, table 3 presents the values obtained for maximum, average, and minimum computation time. In addition, the execution time of the first run of the algorithm is also presented for each group. We can note that computational time is more than 5 hours per route. This is not a problem since the bus routing is not run on a daily bases (operational decision-making process); it is defined only once during the academic year, with possible adjustments each time a student is added or removed from the database.
4.3 Sensitivity analysis
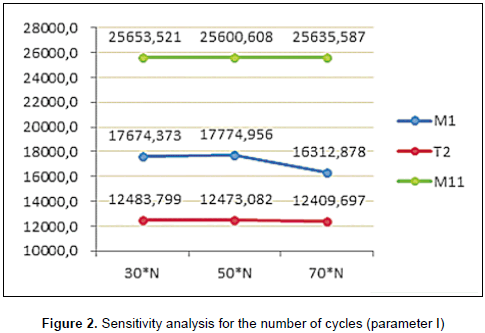
In order to better understand the behavior of the ACO procedure, we carried out a sensitivity analysis on the values of the algorithm parameters. From the total of 22 routes (morning plus afternoon), we selected 3 routes: the first one, noted as M1 (route of Bus 1 in the morning), is chosen because it has the higher number of stops (44 stops); route noted as T2 (route of Bus 2 in the afternoon) is chosen since it has 36 stops corresponding the median value; and finally route noted M11 which corresponds to route of Bus 11 in the morning since it has the lower number of stops (31 stops). The reader may note that the morning route of Bus 8 has only 16 stops, we have not selected it since it already converges for the values of parameters and hence the impact on their variations will not have a significant effect for the purpose of this sensitivity analysis.
For the analysis carried out here, the six parameters of the ACO algorithms were considered: number of cycles (I), number of ants (K), q0, b, r, t0. If one parameter is changed, the others remain constant and their value is the one defined previously in table 2.
Concerning the number of cycles (I), the value defined previously was I=50×N, where N is the number of stops defined for a given bus. For this sensitivity analysis, we tested with 30×N and 70×N. Figure 2 presents the variations obtained for each bus route. It seems that generating more solutions will drive the algorithm to increase its probabilities of obtaining the optimum. However, we observe a convergence of the objective function value and no more improvement is done. Such is the case of routes T2 and M11 for which the solution values with 30×N, 5×N or 70×N cycles is the same. We observe, however, that changing this parameter does have an impact for the case of route M1. No significant difference is observed for the cases with 30×N and 5×N, while the case with 70×N cycles gives a good improvement of the objective value. This is explained by the fact that route M1 is the route with higher number of stops, which may allow the algorithm to propose a higher number of possible solutions and then select the better one among those. At the end, it will be necessary to perform a higher number of cycles to find convergence.
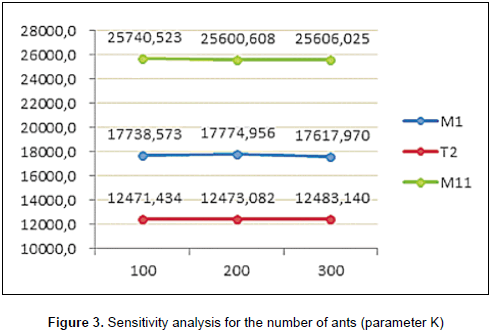
The basic value for the number of ants was defined to be 200 per cycle. For the sensitivity analysis, we also used 100 and 300 ants. Figure 3 presents the comparison between the results obtained. Together with the number of cycles, the number of ants determines the extension of the number of solution that will be evaluated for convergence and from where the best solution will be selected. As in the previous analysis, we observe that solutions for routes T2 and M11 do not present considerable changes when changing the number of ants. In this case, we observe that route M1 does not present a significant difference when changing the number of ants. So, an interesting question would be to know why the number of cycles gives better solutions for route M1 while the number of ants does not. According to Dorigo and Stützle (2004) when the pheromone trace is updated based on the quality of the solution, the algorithm converges faster than when the trace is updated with a constant value. In our model, local updating is performed based on a constant value τo, once an ant finishes the route, while global updating is executed at the end of a cycle based on the distance traveled by the best ant (Lmc). This verifies the statement of those authors. In addition, we can conclude that, for the particular algorithm designed here, it is a better choice to increase the number of cycles than the number of ants when executing the procedure.
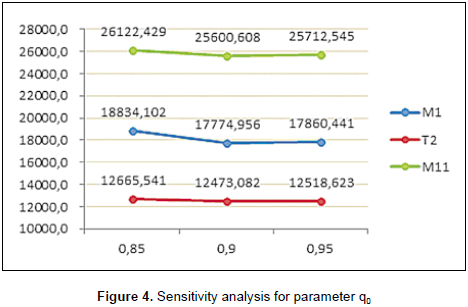
For parameter q0, the original value for the experiments was 0.9. We also tested the values of 0.8 and 0.95. Figure 4 presents the variations obtained by changing only this parameter. We can observe that, even if the variations of the objective function values are not significant, the best value for the three routes is obtained when q0=0.9. This means that in our algorithm an intensification strategy of the current solution is preferred than a diversification strategy.
Looking at parameter β, figure 5 presents the results of two sensitivity experiments. The first (figure 5a) corresponds to a preliminary analysis performed only with routes with the highest number of stops: M1 is Bus 1 morning route, M7 is Bus 7 morning route, and T4 is Bus 4 afternoon route. We can observe a big variation of the objective function value when changing this parameter from 1/3 to 3. However, between β=4 and β=6 the variation is not such significant. We have to recall that β=5 was the value chosen for the experimental analysis. Note that the case of M1 (morning route of Bus 1) when β=6 shows again that the search procedure might fall into local optima. The reduction of 1420.48 m between β=5 y β=6 shows that the higher the number of stops, the higher the impact of the pheromone trace in comparison with the heuristic function.
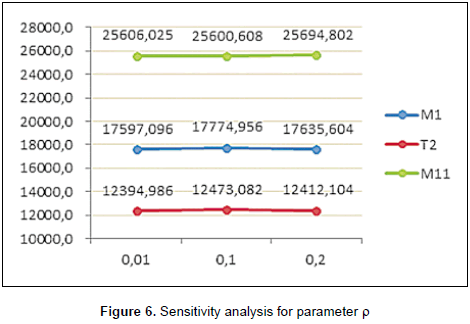
The next analysis was carried out for parameter ρ. We recall that the value employed for the experiments was 0.1. For this analysis, we choose the values of 0.01 and 0.2. Variations on the values of the objective function are presented in figure 6. The value of ρ determines the evaporation speed of the pheromone trace. The higher the value, the faster the pheromone will evaporate and hence the faster the algorithm converges. Since the figure does not show significant differences between values 0.01 and 0.2, it can be stated that the model has a consistent behavior for a broad range of values of ρ.
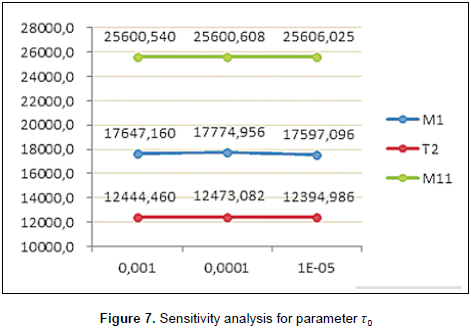
Finally, the last analysis was carried for parameter τo. The value selected for the numerical experiments was 0.0001. Figure 7 also presents the variation of the objective function value for values of τo=0.001 and τo=0.0001. As for the case of parameter ρ, the higher the value of τo, the faster the algorithm converges. This is because the level of pheromone on the arcs visited by the ants will increase drastically.
In summary, the sensitivity analysis shows that some parameters have higher impact on the objective function value than others. It has been observed that increasing the values of I and K may lead to decreasing the total length of routes but this increases the computational time. When the number of solutions is limited, parameter β becomes relevant since it will affect the final value of the objective function in the solution. Parameter q0 showed that intensification is more important than diversification, for the problem under study.
4.4 Financial evaluation
In order to measure the financial impact of the proposed route, we have performed a comparison between the consumption of fuel for the initial current manual routing with that of the proposed solution. We hence collected information about the cost of fuel consumption for the fleet of buses. We observed that the total cost of fuel consumption of the current routing was COP$670.000, and that the average theoretical yield of buses is 4798.48 meters per gallon or 1267.62 m/L. This average yield allows us to compute the daily cost of fuel for the proposed routing. We noted that the total daily cost of the proposed routing was COP$568172. When comparing this value with the current one of the current manual routing, it is possible to compute the total saving for an academic year (table 4). Considering, for instance, the academic year 2010 with a total of 171 class days the annual saving by implementing the proposed ACO routing algorithms would have been COP$17412607, which corresponds to a reduction of 17.9 % on fuel consumption costs. To this we have to add the fact that routes for each bus are shorter, which positively impacts on the total working time of bus drivers, as well as in both the time students have to wake up in the morning and the time students arrive at home in the afternoon.
5. CONCLUDING REMARKS
This paper studied a real-life school bus routing problem. The problem was modeled as a classical capacitated vehicle routing problem. It was solved using a two-phase resolution approach. The first phase consisted in define the assignment of student pickup (or student delivery) points to buses, while the second phase consisted in the actual routing of buses using an ant colony optimization (ACO) based algorithm. This last part was solved as an asymmetric traveling salesman problem. During the resolution, a sensitivity analysis was also carried out to validate the parameters chosen to run the algorithm. The proposed approach found a reduction of 15.2 % of the total cost of student pickup to go to school and then delivery to their home. In addition to cost reductions, the proposed bus routing allows also a reduction on students travel and hence improving their quality of life, since they can arrive at home early in the afternoon. The challenge now is to continue improving the decision-aid tool to allow speeding up the algorithm, as well as additional reductions on travel time and costs in order to positively reduce the impact on the environment (e.g. to reduce CO2 emissions).
REFERENCES
Angel, R. D.; Caudle, W. L.; Noonan, R. and Whinston, A. (1972). "Computer-assisted school bus scheduling". Management Science, vol. 18, No. 6 (February), pp. 279-288. [ Links ]
Bennett, B. T. and Gazis, D. C. (1972). "School bus routing by computer". Transportation Research, vol. 6, No. 4 (December), pp. 317-325. [ Links ]
Bodin, L. D. and Berman, L. (1979). "Routing and scheduling of school buses by computer". Transportation Science, vol. 13, No. 2, pp. 113-129. [ Links ]
Bowerman, R.; Hall, B. and Calamai, P. (1995). "A multiobjective optimization approach to urban school bus routing: Formulation and solution method". Transportation Research Part A, 29, pp. 693-702. [ Links ]
Braca, J.; Bramel, J.; Posner, B. and Simchi-Levi, D. (1997). "A computerized approach to the New York City school bus routing problem". IIE Transactions, vol. 29, No. 8, pp. 693-702. [ Links ]
Chapleau, L.; Ferland, J. A. and Rousseau, J. M. (1985). "Clustering for routing in densely populated areas". European Journal of Operational Research, vol. 20, No. 1, pp. 48-57. [ Links ]
De la Cruz, J. J.; Paternina-Arboleda, C. D.; Cantillo, V. and Montoya-Torres, J. R. (2011). "A two-pheromone trail ant colony system-tabu search approach for the heterogeneous vehicle routing problem with time windows and multiple products". Journal of Heuristics, Available online. DOI: 10.1007/s10732-011-9184-0. [ Links ]
Desrosier, J.; Ferland, J. A.; Rousseau, J. M.; Lapalme, G. and Chapleau, L. An overview of a school busing system. In: Scientific management of transportation systems. Jaiswal, N. K. (ed.). Amsterdam: North-Holland, 1981. Pp. 235-243. [ Links ]
Doerner, K. F.; Hartl, R. F.; Benker, S. and Lucka, M. (2006). "Ant colony system for a VRP with multiple time windows and multiple visits". Parallel Processing Letters, vol. 16, No. 3, pp. 351-369. [ Links ]
Dorigo, M. and Gambardella, L. M. (1996). Solving symmetric and asymmetric TSPs by ant colonies. Proceedings of the IEEE Conference on Evolutionary Computation (ICEC'96), Nagoya, Japan (20-22 May), pp. 622-627. [ Links ]
Dorigo, M. and Gambardella, L. (1997). "Ant colonies for the traveling salesman problem". BioSystems, vol. 43, No. 2 (July), pp. 73-81. [ Links ]
Dorigo, M. and Stützle, T. Ant colony optimization. Cambridge, MA: MIT Press, 2004. [ Links ]
Dulac, G.; Ferland, J. A. and Forgues, P. A. (1980). "School bus routes generator in urban surroundings". Computers and Operations Research, vol. 7, No. 3, pp. 199-213. [ Links ]
Favaretto, D.; Moretti, E. and Pellegrini, P. (2007). "Ant colony system for a VRP with multiple time windows and multiple visits". Journal of Interdisciplinary Mathematics, vol. 10, No. 2, pp. 263-284. [ Links ]
Fügenschuh, A. (2009). "Solving a school bus scheduling problem with integer programming". European Journal of Operational Research, vol. 193, No. 3 (March), pp. 867-884. [ Links ]
Gajpal, Y. and Abad, P. (2009). "An ant colony system (ACS) for vehicle routing problem with simultaneous delivery and pickup". Computers and Operations Research, vol. 36, No. 12, pp. 3215-3223. [ Links ]
Laporte, G. (1992). "The vehicle routing problem: An overview of exact and approximate algorithms". European Journal of Operational Research, vol. 59, No. 3 (June), pp. 345-358. [ Links ]
Li, L. and Fu, Z. (2002). "The school bus routing problem: A case study". Journal of the Operational Research Society, vol. 53, pp. 552-558. [ Links ]
Martínez, L. M. and Viegas, J. M. (2011). "Design and deployment of an innovative school bus service in Lisbon". Procedia - Social and Behavioral Sciences, vol. 20, pp. 120-130. [ Links ]
Newton, R. M. and Thomas W. H. (1969). "Design of school bus routes by computer". Socio Economic Planning Sciences, vol. 3, No. 1, pp. 75-85. [ Links ]
Park, J. and Kim, B.-I. (2010). "The school bus routing problem: A review". European Journal of Operational Research, vol. 202, No. 2 (April), pp. 311-319. [ Links ]
Riera-Ledesma, J. and Salazar-González, J. J. (2012). "Solving school bus routing using the multiple vehicle traveling purchaser problem: A branch-and-cut approach". Computers and Operations Research, vol. 39, No. 2, pp. 391-404. [ Links ]
Spada, M.; Bierlaire, M. and Liebling, T. M. (2005). "Decision-aiding methodology for the school bus routing and scheduling problem". Transportation Science, vol. 39, No. 4 (November), pp. 477-490. [ Links ]
Tan, X.; Luo, X.; Chen, W. N. and Zhang, J. (2005). "Ant colony system for optimizing vehicle routing problem with time windows". Proceedings of the International Conference on Intelligent Agents, Web Technologies and Internet Commerce, Vienna, Austria (28-30 November), vol. 2, pp. 209-214. [ Links ]