INTRODUCCIÓN
Las meta-heurísticas (Glover, 2008) basadas en población desde su aparición representan una herramienta muy apropiada para resolver problemas discretos. Estos algoritmos utilizan una población (conjunto de soluciones) para explorar el espacio de búsqueda complejo que supone la optimización combinatoria. El problema del Viajero Vendedor (también conocido como problema del Viajante de Comercio o por sus siglas en inglés: TSP) (Johnson, 1997) es uno de los problemas más famosos (y quizás el mejor estudiado) en el campo de la optimización combinatoria.
Desde el punto de vista práctico, el problema no está resuelto y desde el punto de vista teórico, las técnicas empleadas son sólo aproximaciones. Estas no suponen una resolución real del TSP y sólo ofrecen soluciones aproximadas suficientemente aceptables. Por otra parte los algoritmos clásicos no son capaces de resolver el problema general, debido a la explosión combinatoria de las posibles soluciones. Por ello, a su solución se han aplicado distintas técnicas meta-heurísticas (Michalewicz, 2004).
Las metaheurísticas poblacionales han sido las más aplicadas a la solución del TSP. Estos algoritmos trabajan sobre un conjunto de soluciones potenciales, llamada población, y realizan la exploración del espacio de búsqueda a través de la cooperación y competencia entre las soluciones potenciales; ejemplos de estas técnicas son los Algoritmos Genéticos (Genetic Algorithms, GA) (Golberg, 1998), la Optimización basada en Colonias de Hormigas (Ant Colony Optimization, ACO) (Dorigo, 2004) y la Optimización basada en Enjambres de Partículas (Particle Swarm Optimization, PSO) (Eberhart, 1995).
En trabajos anteriores se presentó la Optimización basada en Malla Variable (VMO) (Puris, et al., 2012) como una meta-heurística eficiente para problemas de optimización contínua. VMO utiliza una población conocida como malla para explorar el espacio de búsqueda. Esta malla se expande (incorporando nuevas soluciones) utilizando distintas formas de generación de soluciones. Finalmente, la malla es reducida utilizando un operador de limpieza adaptativo (clearing) que elimina todo nodo o solución que se encuentre cerca de otro de mejor calidad (fitness). Este algoritmo ha presentado soluciones competitivas en problemas continuos con diferentes características: aproximación de funciones multimodales (Puris, et al., 2012), problemas de nichos (Molina, et al., 2013), óptimos en las fronteras (Navarro, et al., 2009); pero, no se conoce de algún estudio previo sobre la aplicación de esta técnica en problemas de optimización combinatoria.
En este trabajo presentamos una adaptación de VMO orientada a explorar espacios discretos. Específicamente se aplica a la solución de diferentes instancias del TSP como una referencia obligatoria para probar la efectividad de nuevos algoritmos. Además, se incorpora un método de búsqueda local (BL) con el objetivo de explorar detalladamente los entornos de las zonas más prometedoras y hacerlas más representativas. Para finalizar el estudio, se hace una comparación entre los resultados alcanzados por la propuesta de VMO y tres algoritmos basados en Colonias de Hormigas (ACS, AS, MMAS) (Dorigo, 2004).
MATERIALES Y MÉTODOS
El Viajante de Comercio (Johnson, 1997), puede ser representado como un grafo completo G = (N, A), donde N representa la cantidad de nodos también llamados ciudades y A el conjunto de arcos bidireccionales que conectan los nodos. Cada acro a se le asigna un valor dij que representa la distancia entre las ciudades i y j. El objetivo de este problema radica en encontrar el camino (ciclo hamiltoniano) más corto desde una ciudad de partida, pasando por todas las demás ciudades solo una vez y regresando a la ciudad de origen. En el caso del TSP simétrico las distancias entre las ciudades son independientes de la dirección de la ruta (d=dj). Todas las instancias utilizadas para el estudio experimental de este trabajo son tomadas de la biblioteca pública TSPLIB (Reinelt, 1991) y son detalladas en el apartado de los resultados experimentales.
Optimización basada en Mallas Variables
VMO es una meta-heurística poblacional en la que la población se distribuye como una malla de nodos (n1, n2, ..., nP) que representan soluciones en el espacio de búsqueda. La exploración se lleva a cabo por dos procesos: de expansión y de contracción (Puris, et al., 2012). El proceso de expansión genera nuevos nodos utilizando la población en la iteración actual, por medio de los pasos siguientes:
Fase 1 (Generación de la población inicial): Se generan P soluciones factibles de manera aleatoria que representan los nodos de la malla inicial en el proceso de búsqueda del algoritmos.
Fase 2 (Generación de nodos hacia los mejores vecinos): Para cada solución de la malla (ni) se buscan los k nodos más cercanos. A continuación se selecciona el vecino de mejor calidad (fitness) (n*), y si n* es mejor que ni se genera un nuevo nodo entre ambos; caso contrario, no se genera una nueva solución.
Fase 3 (Generación de nodos hacia la mejor solución): Se crea un nuevo nodo para cada ni en dirección al nodo con mejor valor de fitness (ng, óptimo global) de la malla actual.
Fase 4 (Generación de nodos utilizando los nodos fronteras de la malla): Los nodos fronteras se definen como las soluciones que se encuentran más cerca y más lejos del centro de la población. En esta fase las nuevas soluciones se generan desplazando cada nodo frontera en función de un valor de desplazamiento w (Puris, et al., 2012).
Fase de Clearing: En esta fase, se seleccionan las soluciones más representativas entre la malla actual y los nuevos nodos generados en el proceso de expansión (Fase 2, 3, 4). Para ello, se evita seleccionar soluciones demasiado cercanas entre sí. Durante el clearing se define una distancia % como distancia mínima entre las soluciones, y se tiene que ignorar todo nodo que tenga una distancia inferior a un nodo con mejor o igual calidad. Dicha distancia se inicializa a un 25% del rango de búsqueda, y va reduciéndose durante la ejecución del algoritmo (Puris, et al., 2012).
En el próximo apartado se definirá cada uno de los operadores de generación de nodos utilizados para el caso de estudio del TSP y la forma en que se realiza la operación de clearing.
VMO para el TSP
Aunque la definición general de la meta-heurística VMO no está dirigida exactamente para un tipo de dominio, se puede decir que sus operadores de expansión utilizan formas de generación de nuevas soluciones siguiendo un enfoque contínuo (más información en (Puris, et al., 2012)), por lo que a continuación se redefinen cada unos de ellos para adaptarlos a la generación de soluciones en dominios discretos.
Generación de la malla inicial
En este paso se generan P soluciones factibles de forma aleatoria. Cada nodo se genera considerando que no se puede asignar una misma ciudad en las diferentes posiciones, de manera que un nodo representa un camino o ciclo hamiltoniano desde cualquier ciudad de origen (también seleccionada de manera aleatoria entre todas las ciudades). A continuación se representan los casos posibles de una solución donde se representa el caso a) como favorable ya que no se repite ninguna ciudad en el trayecto, y el caso b) en el cual se puede apreciar que la ciudad 1 se repite por lo que no representa una solución factible para el problema.
Generación de nodos hacia los mejores vecinos
En este paso de generación se utiliza la distancia de Hamming para obtener los k vecinos más cercanos de cada nodo ni de la malla, luego se selecciona entre los k vecinos el recorrido de menor distancia n* (nodo de mejor calidad) y si este representa una mejor solución que el nodo ni se creará una nueva solución a través de una combinación entre ambas soluciones (ni n*) de la siguiente manera:
Generación de nodos hacia la mejor solución global
Para generar nuevas soluciones utilizando este paso primero se selecciona el nodo que representa el recorrido de menor distancia (ng, óptimo global), luego se aplica el algoritmo de la figura 3 (cambiando n* por ng) para generar nuevas soluciones entre cada nodo de la malla inicial y el nodo ng.
Generación de nodo a partir de las fronteras de la malla
En este paso se seleccionan los nodos o soluciones que representan las fronteras de la malla inicial, esto se lleva a cabo utilizando la distancia de Hamming para crear una matriz simétrica de distancias entre nodos. Luego se selecciona como frontera interior al nodo que más cerca se encuentre de los demás y como frontera exterior el que más lejano se encuentre. Luego a estos nodos se les realiza una permutación de dos posiciones seleccionadas de manera aleatoria.
En la propuesta original de VMO se seleccionan como frontera interior y exterior una cantidad de nodos necesarios para completar la cantidad de soluciones de la malla total. En nuestra propuesta solo se selecciona una solución por cada conjunto.
Operador de clearing
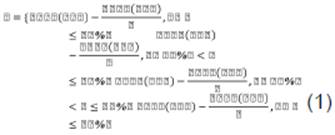
Para el caso de estudio, en este operador se ordena de manera ascendente los nodos en función de la calidad del recorrido que representan, luego se eliminan aquellas soluciones que estén a una distancia de Hamming menor que ξ de otro nodo de mejor calidad. La ecuación 1 presenta la forma de calcular ξ dónde size (TSP) representa la cantidad de ciudades de la instancia que será computada, C es la cantidad total de iteraciones que realizará el algoritmo (parámetro de VMO) y c la interacción que se está ejecutando en el momento del cálculo de la distancia, cumpliendo que c ≤ C.
El conteo aplicado por la distancia de Hamming no se realiza posición a posición como lo propone el algoritmo original; sino, por secuencias de tamaño 2.
Aplicación de la búsqueda local
Los procedimientos de búsqueda local comienzan con una solución del problema y la van mejorando progresivamente. El procedimiento realiza en cada paso un movimiento de una solución a otra con mejor valor. El método finaliza cuando en un estado no existe ninguna solución accesible que la mejore. Para el caso del TSP existen diferentes algoritmos de búsqueda local entre los que destaca el Recocido Simulado (Gellat, et al., 1983), Búsqueda Tabú (Glover & Laguna, 1997), Lin y Kernighan y los conocidos k-intercambios (StützleH & Hoos, 1997). Entre este último el algoritmo 2-intercambio (2-opt) (StützleH & Hoos, 1997), (San Lucas, Tolozano, 2018) es de los más simples y utilizados en la literatura para hibridar con Meta-heurística poblacionales. En la presente investigación se propone utilizar este algoritmo para aplicarlo a cada una de las soluciones obtenidas en los operadores de generación de nodos del algoritmo VMO.
RESULTADOS
En esta sección se ha preparado un estudio experimental para probar el desempeño de la propuesta VMO para la solución de diferentes instancias del TSP (bays29, st70, rd100, ch150, kroA200, tsp225, a280, lin318, pcb442) (Reinelt, 1991), donde el número que aparece en el nombre de estas, representa la cantidad de ciudades que tiene la instancia.
A continuación se detallan los experimentos realizados para ajustar los parámetros del algoritmo VMO los cuales son P tamaño de la malla inicial, k cantidad de nodos que conforman la vecindad y C la cantidad de iteraciones que ejecutara el algoritmo. Luego una comparación con los resultados obtenidos por tres algoritmos de la metaheurística ACO (Ant Colony System (ACS), Ant System (AS) y MaxMin Ant System (MMAS)) (Dorigo, 2004) como uno de los modelos poblacionales que mejores soluciones ha presentado al TSP.
Para comprobar los experimentos se ha utilizado un conjunto de técnicas estadísticas no paramétricas propuestas en (García, et al., 2007) como una herramienta para comparar resultados obtenidos por métodos aproximados. En la discusión de los resultados se describe el test utilizado y la forma de interpretar los resultados de estos.
Tamaño de la malla inicial
A diferencia de la propuesta original de VMO donde se estudia la relación directa entre el tamaño de la población inicial y el tamaño máximo de la expansión, en este caso solo se estudiará la influencia del tamaño de la población inicial en la evolución del algoritmo (8, 12, 24).
Como se puede apreciar en la Tabla 1, el valor p obtenido por el test de Iman-Davenport para detectar diferencias en el grupo formado por las tres variantes estudiadas (VMO(8), VMO(12), VMO(24)) es menor que el valor a de significancia del test, por lo que la hipótesis de semejanza es rechazada, concluyendo que existen diferencias significativas entre los resultados computados.
Tabla 1: Resultados del test Iman-Davenport con α=0.05.
| Método | Valor del Test | Valor p | Hipótesis |
|---|---|---|---|
| Iman-Davenport | 5.066 | 1.76E-13 | Rechazada |
Fuente: Autores.
Para el caso a continuación se aplica un test de Holm, tomando como muestra de control los resultados alcanzado por VMO(24). Esta selección se lleva a cabo porque es el que mejor valor medio obtuvó.
Como se puede apreciar en la Tabla 2, el test de Holm detecta diferencias significativas entre la muestra de control (VMO(24)) y cada una de otras variantes comparadas. Esto se evidencia porque los valores p de cada algoritmo es menor que su correspondiente valor a/i, rechazando la hipótesis de semejanza en cada una de las comparaciones.
Tabla 2 Resultados del test de Holm para un valor a=0.05.
| Algoritmo | Z | Valor p | a/i | Hipótesis |
|---|---|---|---|---|
| VMO(8) | 2.999 | 7.74E-6 | 0.025 | Rechazada |
| VMO(12) | 1.999 | 0.02534 | 0.05 | Rechazada |
Fuente: Autores.
De este análisis se puede concluir que los resultados alcanzados utilizando una malla inicial de tamaño 24 obtiene resultados significativamente mejores que las otras variantes de configuración de malla inicial.
Cantidad de vecinos utilizados en la Face 2
Este parámetro es utilizado en la propuesta para determinar la cantidad de soluciones que conforman la vecindad de un nodo n. En este experimento se probaron diferentes valores 3 y 5 que son los propuestos por los autores en el estudio desarrollado en (Puris, et al., 2012).
A continuación la Tabla 3 presenta los resultados del test de Wilcoxon para comparar ambas propuestas, donde se puede apreciar que existen diferencias significativas a favor de la propuesta que utiliza 5 vecinos para la face 2 de VMO. Esto se puede evidenciar a partir de que el valor p es menor que el valor de significancia aplicado al test rechazando la hipótesis de igualdad.
DISCUSIÓN
Comparación con Sistema de Colonia de Hormigas
A continuación se realiza una comparación entre los resultados obtenidos en esta investigación y uno de los algoritmos de la metaheurística ACO (Sistema de Colonia de Hormigas; ACS) que más ha sido estudiado en la solución del TSP. En ambos casos fueron ejecutados los algoritmos para la misma cantidad de iteraciones 1000*F, donde F representa el tamaño de la instancia del TSP utilizada y además ambos algoritmos utilizaron la búsqueda local 2-opt. La configuración de parámetros y los resultados de ACS, MMAS y AS fue la utilizada en (Puris, et al., 2010).
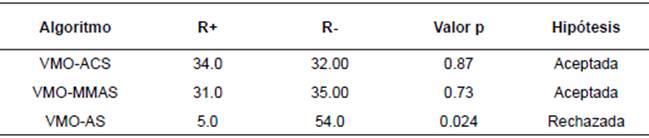
La Tabla 4 muestra los resultados del test de Wilcoxon donde se puede apreciar que el valor p es mayor que a para las comparaciones con los algoritmos ACS y MMAS por lo que la hipótesis de igualdad es aceptada. De estos se concluye que no existen diferencias significativas entre la calidad de los resultados obtenidos por ambos algoritmos y VMO para el TSP. Para el caso de la comparación con el algoritmo AS se puede apreciar que la hipótesis es rechazada a favor VMO demostrando que los resultados alcanzados por este algoritmo son significativamente mejores que los obtenidos por AS.
CONCLUSIONES
Como conclusión de esta investigación se desarrolló una propuesta para aplicar la meta-heurística VMO al problema discreto TSP que difiere del modelo original en los siguientes aspectos:
Se aplicaron otros operadores de generación de nuevos nodos en el proceso de expansión, donde se realiza una combinación de soluciones de manera que cumpla con las restricciones impuestas por el problema.
Se aplicó una variante de la distancia de Hamming donde se comparan secuencias de tamaño 2 para realizar el operador de clearing con el objetivo de eliminar soluciones que compartan la mayor cantidad de secuencias iguales.
Solo dos soluciones forman el conjunto frontera donde se identifican como las más y menos semejantes a los demás nodos de las mallas. Luego se perturban las soluciones a través de simples permutaciones internas en dichos nodos.
Se aplicó el algoritmo de búsqueda local 2-opt a cada solución generada en el proceso de expansión con el fin de mejorar las soluciones obtenidas.
Se realizó un estudio de los parámetros, tamaño de la malla (P) y tamaño de la vecindad (k), donde se obtuvieron los mejores resultados para un valor de P=24 y k=5 entre los valores probados.
Finalmente se realizó un estudio comparativo entre los resultados alcanzado por la propuesta VMO y tres de los principales algoritmos de la meta-heurística poblacional ACO. De este estudio se pudo concluir que el algoritmo VMO obtiene resultados semejantes a los encontrados por los algoritmos ACS y MMAS y mejores que la variante AS. Estos resultados son muy importantes al ser la primera investigación que se realiza con VMO para un problema discreto y de tanta complejidad como el TSP, quedando abiertas líneas de trabajo en este tema.