Gerardo de Jesús Montoya Gaviria

Departamento de Geociencias, Universidad Nacional de Colombia Bogotá E-mail: gdmontoyag@unal.edu.co

ABSTRACT

Usually, it is assumed in the continuous growth equation by coalescence, that mass and terminal velocity of the collected drops are negligible in comparison with the mass and velocity of the collector drop. These assumptions, which are reasonable in warm cloud modeling, appear to be not so adequate for mixed phase clouds, where interactions between different categories (cloud water, rain water, crystal ice, graupel, hail) have to be considered.

When the above constraints are removed, new particular solutions of the continuous growth equation arise, which are presented in this paper. Two solutions are obtained by assuming a gamma droplet distribution. The first solution is obtained for a terminal velocity that is approximated by a power-law, while the second derives from a polynomial approximation.

These solutions may be of interest for use with explicit microphysical parameterizations in mesoscale models

Key words: Coalescence, Continuous growth, clouds, precipitation.

RESUMEN

En la ecuación de crecimiento continuo por coalescencia usualmente se asume que la masa y la velocidad de caída de las gotas capturadas es despreciable en comparación con la masa y la velocidad de la gota colectora. Estas hipótesis, las cuales son razonables en modelación de nubes calientes, no es tan adecuada para nubes mixtas donde se considera interacción entre diferentes categorías (agua de nube, de lluvia, cristales de hielo, nieve pedriscos y granizo).

Cuando esta limitación es removida de la ecuación, se obtiene nuevas soluciones, dos de las cuales se presentan en este trabajo. Ambas soluciones se obtuvieron asumiendo una distribución gamma, la primera de ellas para una velocidad de caída de tipo potencial y la segunda para una aproximación polinomial de esta variable.

Estas soluciones pueden ser de utilidad para la parametrización de la microfísica explicita dentro de modelos de mesoescala.

Palabras Claves: cualescencia, crecimiento contínuo, nubes, precipitación.

INTRODUCTION

One of the mechanisms leading to the growth of cloud droplets and the subsequent development of precipitation is gravitational coalescence. The accurate representation of this process is essential for the success of any parameterization scheme of microphysical processes in clouds and mesoscale models.

There are several approaches to the calculation of droplet growth by coalescence actually used in atmospheric models: one kind of approach involves the solution of the kinetic equation, see for example Berry and Reinhardt (1974), and Tzivion et al. (1987). Application of such a method within a fully tridimensional mesoscale model still demands prohibitive computational resources. Another method involving solutions for this equation was developed by Verlinde et al. (1980) and actually used in the RAMS model. However, the last method requires the use of “look up” tables, increasing with this, computational needs. Also, it is not clear how this method performs regarding the coalescence between categories of similar sizes.

To a second kind of approach belong the methods based on the continuous growth equation. Due to its simplicity, this equation was used initially by Kessler (1969) and other authors to simulate warm rain processes and later by Rutledge and Hobbs (1983), Lin et al. (1983), and other authors, for mixed-phase cloud computations.

It is assumed, in the continuous growth equation used in these works, that the mass and terminal velocity of the collected particles (for instance, cloud drops) are negligible in comparison with the mass and terminal velocity of the collector particle (rain drops, for example).

Also, in many schemes it is assumed that the particles are distributed within the cloud and precipitation environment according to the power law first proposed by Marshall & Palmer (1948):

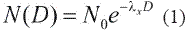
where, N(D) is a number density (number of drops of diameter D per unit volume per unit size interval), N₀ is the intercept, and λ is the inverse of the mean drop diameter D_mx.

Furthermore, in several schemes it is assumed that the particles fall with terminal velocity of power-law type of the form:

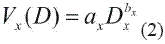
where, D is particle diameter, a_x and b_x are empirical adjustmentparameters and the subscript x represents any category (cloud, water, rain water, cloud ice, etc.). According to Reisner et al. (1998), for rain drops (x=r), ar =842 sec-1 and br =0.8.

The above-mentioned assumptions are valid for a parameterization of warm rain processes, and when the precipitation stage already exists. However, for mixed-phase clouds, where interactions between more than two categories (cloud water, rain water, cloud ice, snow, graupel, hail, etc.) take place, disregarding the mass and terminal velocity of the collected particle may lead to inaccuracies in the computation of the precipitation rate.

Some actual mesoscale models, as the one used by the Japanese meteorological office (see Murakami, 1990, Ikawa and Saito, 1990), the Canadian mesoscale, and the MM5 models (see Reisner et al, 1998), base their parameterization schemes on the ideas of Rutledge and Hobbs (1983), Lin e.a (1983), and other authors.

Thus it is appropriate to derive the continuous growth equation by removing the above-mentioned assumptions.

In this work, two new forms of the continuous growth equation are derived that have not been presented in the literature. They were obtained assuming a gamma distribution and by retaining the mass and terminal velocity of the collected particles. The first solution is obtained assuming a power-law terminal velocity, and the second for a polynomial approximation. In the following section, basic assumption are made. Next, the general form of the continuous growth equation will be presented, the solution for a power-law terminal velocity will then be obtained, and finally, in section 5, the solution for the polynomial approximation will be derived.

BASIC ASSUMPTIONS

In contemporary models, a more general distribution function is used - the gamma function:

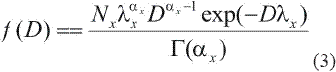
where N_x is the drop concentration per unit volume (m-3), and G the gamma function with α_x as a free parameter and λ_x named the slope parameter for the category x, is related to α_x and the mean diameter by the relation:

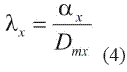
It is easy to show, through the moments of the distribution (3), that for α_x = 1 and

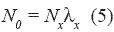
the distribution (3) reduces to the Marshall & Palmer distribution (1).

It is also not difficult to show that for the distribution (3) the expression for the mixing ratio can be written in the form;

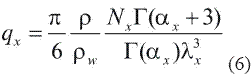
where ρ and ρ_w are the densities of air and water respectively.

Empirical studies have shown that the terminal velocity for large drops is better represented by a polynomial approximation rather than by a power law, as suggested by Rutledge and Hobbs (1983):

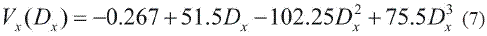
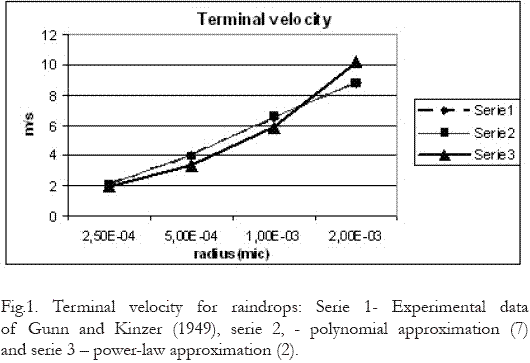
Figure 1 shows a comparison between the relations (2) and (7) and the experimental data of Gunn & Kinzer (1949). The Figure clearly shows that the polynomial approximation fits the observational data of Gunn & Kinzer better than the power-law approximation, specially for large raindrops.

GENERAL FORM OF THE CONTINUOUS GROWTH EQUATION

The increase in volume of a collector particle of radius Rx falling within an environment of smaller cloud particles of radius Ry and fall velocity u(R_y) reads (see for instance Rodgers & Yau, 1979):

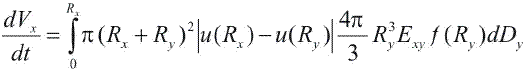
where f(R_y) is the distribution of the smaller particles and E_xy is the coalescence coefficient.

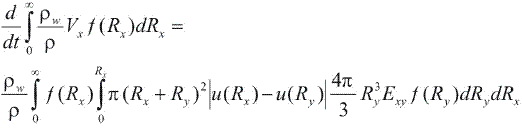
Assuming that R_x >R_y, this expression may be written as,

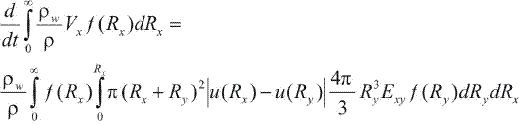
This equality may be written as a function of the diameter D instead of the radius using the conservation condition, f(R)dR=f(D)dD. Then for D_x > D_y.

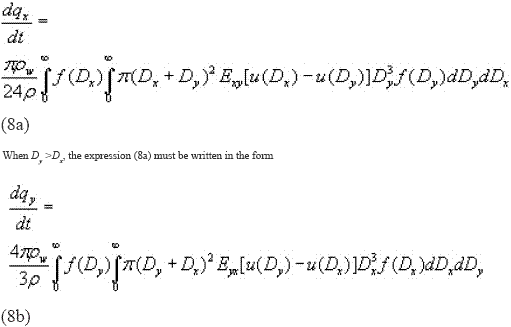
The expressions (8a) y (8b) represent the general form of the continuous growth equation by coalescence.

The expression presented in Rutledge and Hobbs (1983) for continuous growth, may be obtained from (8a), neglecting the radius and terminal velocity of the collected particles. The following derivations will be presented only for the case D_x >D_y.

EQUATION FOR THE CONTINUOUS GROWTH FOR THE POWER-LAW VELOCITY APPROXIMATION

Expanding in the expression (8a) the difference and then the square of the sum, the following expression is obtained,

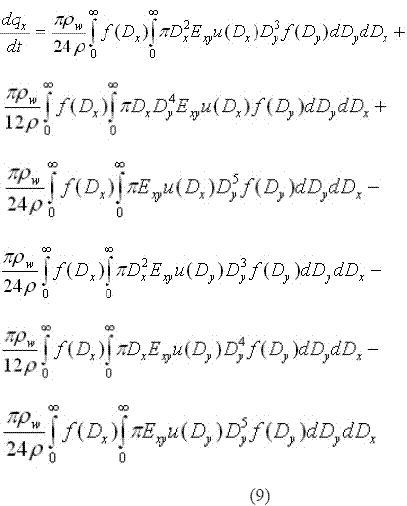
Replacing into this expression the distribution (3) and the terminal velocity (2), and using the definition of the gamma function for a mean collision coefficient, the following expression is obtained in terms of the mixing ratio:

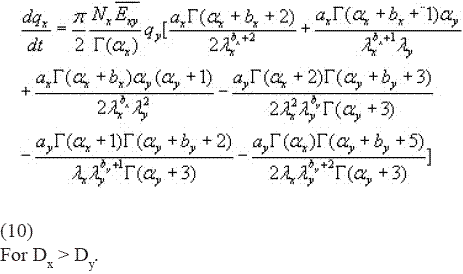
If the gamma distribution reduces to a Marshall – Palmer law thus, the correctness of this expression in the limit can be confirmed: indeed, if the above assumptions are retained, only the first term is conserved and for a=1 we obtain:

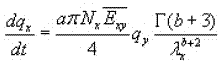
Taking now into account the equality (5), the following expression is obtained:

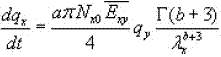
which is the common equation used by Rutledge and Hobbs (1983) and other authors, when a Marshall – Palmer law and power-law approximation to fall velocity is assumed.

EQUATION FOR THE CONTINUOUS GROWTH WITH THE POLYNOMIAL APPROXIMATION

Replacing into (8a) the polynomial form (7) and realizing that the integrals preceded by the coefficient 0.267 disappear, the following expression is obtained,

Replacing now the distribution (3) in each of these integrals and taking into account the definition of the gamma function, again in terms of the mixing ratio, after some rearrangements the following expression is obtained:

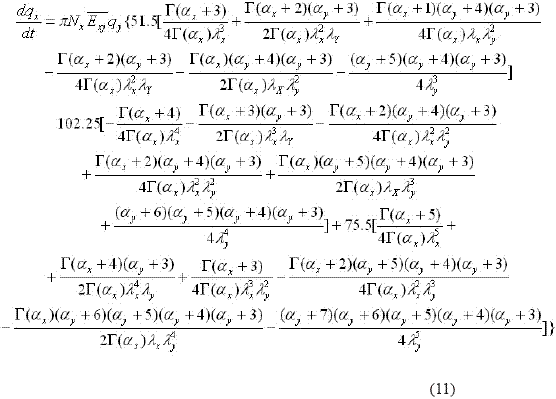
When the radius and fall velocity of the collected drops are negligible, only the first terms appear as well as the term with the coef- ficient 0.267. Thus, the above expression is written as This equation is similar to the one presented by Reisner et al. (1998).

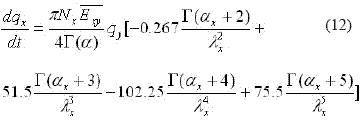
CONCLUSIONS

Two new solutions for the continuous growth equation were obtained for the case when neither the mass nor the terminal velocity of the collected particles may be neglected. The first solution was obtained for a power-law approximation of the fall velocity and the second one with a polynomial approximation.

These solutions may be of interest for use in mesoscale models with explicit but simplified microphysical parameterizations.

ACKNOWLEDGMENTS

This work was supported by the Research Division, DIB, of the National University of Colombia. The author thanks the corrections and suggestions of anonymous reviewers for the final presentation of the manuscript.

REFERENCES

Gunn, R., & G.D. Kinzer 1949: The terminal velocity of fall for water droplets at stagnant air. J. Meteorol., 6, p. 243- 248.        [ Links ]

Kessler, E. 1969: on the distribution and continuity of water substance in atmospheric circulation, Meteorol. Monograph. 10. N. 32, 84 pp.        [ Links ]

Ikawa, M & K. Saito 1990: Description of a non hydrostatic model developed at the forecast research department of the MRI. Tech. Report of the meteorological research institute No 28, 256 pp.        [ Links ]

Levin, L.M., 1958: Sobre las funciones de distribución de las gotas en las nubes y la precipitación. Izvestia academi Nauk CCCP, seria geofísica, No 10, p. 1211-1221.        [ Links ]

Lin, Y. L., R.D. Farley and H.D. Orville 1983: Bulk parameterization of snow field in a cloud model. J. Appl. Meteorol., 22, 1065-1092.        [ Links ]

Marshall, J.S. & W.M: Palmer 1948: The distribution of raindrops with size. J. Meteorol., 5, p. 165-166.        [ Links ]

Murakami, M 1990: Numerical modeling of the dynamical and microphysical evolution of an isolated convective cloud the 19 Juli 1981 CCOPE cloud. J. Met. Soc. Jpn, 68, p.107-128        [ Links ]

Pruppacher, H. R., & J.D. Klett 1997: Microphysics of clouds and precipitation, Sec. Edition, Kluwer Acad. Publishers, 954 pp.        [ Links ]

Reisner, J, R.M: Rasmussen & R.T. Bruintjes 1998: Explicit forecasting of supercooled water in winter storms using MM5 mesoscale model. Q.J.R. Meteorol. Soc. 124, p 1071-1107.        [ Links ]

Rogers, R.R., & M.K. Yau 1989: A short course in cloud physics. Pergamon Press, Second Ed. 292 pp.        [ Links ]

Rutledge, S.A., and P.V. Hobbs 1983: The mesoscale and microscale structure and organizations of clouds and precipitation in midlatitude cyclones Part VIII A model for the seeder feeder process in warm-frontal rainbands. J. Atmos Sci., 40, 1185-1206.        [ Links ]