A simple proof of Abel's theorem on the lemniscate

Solanilla, Leonardo; Palacio, Óscar; Hernández, Uriel

Services on Demand

Journal

Article

Indicators

Cited by SciELO
Access statistics

Ingeniería y Ciencia

Print version ISSN 1794-9165

ing.cienc. vol.6 no.12 Medellín Jan./June 2010

A simple proof of Abel's theorem on the lemniscate

Uma prova simples do teorema de Abel sobre a lemniscata

Demostración simple del teorema de Abel sobre la lemniscata

Leonardo Solanilla¹, Óscar Palacio²y UrielHernández³

1 Doctor en Matemáticas, leonsolc@ut.edu.co, profesor, Universidad del Tolima, Ibagué- Colombia.

2 Profesional en Matemáticas con énfasis en Estadística, tikomania86@hotmail.com, estudiantede Especializaciónen Matemáticas, Universidad del Tolima, Ibagué-Colombia.

3 Profesional en Matemáticas con énfasis en Estadística, uriel501@hotmail.com, estudian te de pregrado, Universidad del Tolima, Ibagué-Colombia.

(Recepción: 27-feb-2010. Modificación: 19-oct-2010. Aceptación: 06-dic-2010)

Abstract

Since Abel's original paper of 1827, his remarkable theorem on the constructibility of the lemniscate splitting has been proven with the aid of Elliptic Functions. Nowadays, Rosen's proof of 1981 is considered definitive. He also makes use of (modern and more elaborate) Class Field Theory.Here we present a novel, short and simple proof of Abel's Theorem on the lemniscate and its converse. Our only ingredients are the addition formulas of Gauss lemniscatic functions and some basic facts of Galois Theory.

Key words:Abel's theorem on the lemniscate, Gauss lemniscatic functions, geometric constructions

Resumo

Desde o artigo original de Abel em 1827, seu notável teorema sobre a construtibilidade da divisão da lemniscata tem sido provado com ajuda das funções elípticas. Hoje, a prova de Rosen (1981) é considerada definitiva. Ele também faz uso da moderna e mais elaborada teoría dos corpos de classes. Neste trabalho, nós apresentamos uma prova nova, curta e simples do Teorema de Abel sobre a lemniscata e seu recíproco. Nossos ingredientes são apenas as fórmulas de adição das funções lemniscáticas de Gauss e alguns fatos básicos da teoría de Galois.

Palavras chaves: teorema de Abel sobre a lemniscata, funções lemniscáticas de Gauss, construções geométricas.

Resumen

Desde la publicación original de Abel en 1827, su notable teorema sobre la constructibilidad de la división de la lemniscata se ha demostrado con ayuda de la teoría de las funciones elípticas. La prueba dada por Rosen en 1981 se considera, hoy por hoy, como definitiva. En ella se utiliza, además, la moderna e intrincada Class Field Theory. Aquí se presenta una demostración nueva, corta y simple del teorema de Abel para la lemniscata junto con su recíproco. Las únicas herramientas son las propiedades aditivas de las funciones lemniscáticas de Gauss y algunos elementos de teoría de Galois.

Palabras claves: teorema de Abel sobre la lemniscata, funciones lemniscáticas de Gauss, construcciones geométricas.

1 Introduction

In 1801, Gauss [1, section 7] proved his celebrated theorem on the construction of the regular polygons by using the trigonometric or circular functions. He also announced that the theory applies to a wider class of transcendental functions including the lemniscatic arc length. Some years later, Abel [2, pp. 361-362] showed indeed clearly his famous theorem. More recently, Rosen [3, p. 388] has claimed to be the first of having the converse of Abel's theorem appeared in print. In what follows, we prove comprenhensively the theorem and its converse from very elementary facts. Our proof improves substantially the technique employed by Hernández and Palacio [4, chapter 4].

Theorem 1.1. The lemniscate can be divided into n equal arcs by means of a compass and an unmarked straightedge if and only if n = 2^kp₁p₂· · · p_t,where the 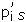are distinct Fermat primes.

In section 2 we define the lemniscate, discuss its arc length and recast the lemniscatic functions to fit the later work. In section 3 we give our proof of the "if " part of theorem 1.1 by examining the Galois group of a suitable extension of Q(i).Section 4 is devoted to the "only if " part of the theorem.At the end we draw some conclusions regarding the possibility of generalizing the procedure to a whole class of curves comprising the circle and the lemniscate.

2 Gauss lemniscatic functions

Here, the lemniscate is the locus L of points (x, y) in the plane satisfying the equation (x² + y²)²= x²− y². In polar coordinates (r, θ), the equation becomes r²= cos 2θ and its arc length is given by the function

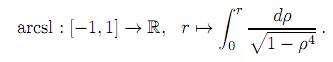
The lemniscatic sine sl(x) is the odd function resulting from extending arcsl^-1to the real line in such a way it is periodic with period 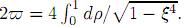The lemniscatic cosine is cl(x) = sl .

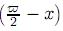The most important properties of the lemniscatic functions are their addition formulas

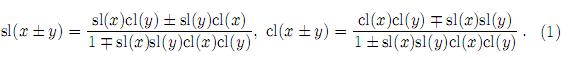
By induction on n ∈ Z⁺,

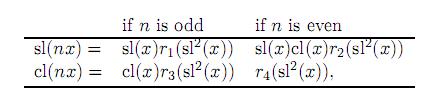
where r₁, r₂, r₃, r₄ stand for rational functions in one in determinate with integer coefficients.

The Pythagorean-like identity

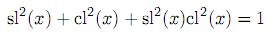
can be visualized as the image C of the map x 7→ cl(x), sl(x) . Figure 1 shows a sketch of this curve. C possesses a canonical group structure isomorphic to

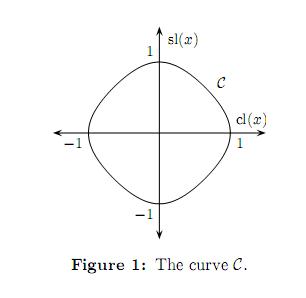
the quotient 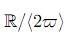of the additive group R into the subgroup generated by .

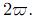Since every point (sl(x), cl(x)) ∈ C determines clearly a (x, y) ∈ L and the critical point of the lemniscate introduces no confusion,we may use C to split the lemniscate L. For a fixed positive integer n, our problem is then equivalent to the constructibility of the division points γ_k =cl 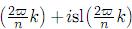∈ C, k = 0, 1,...,n −1.The addition formulas (1) provide Γ_n= 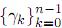with a natural

k = 0 group structure isomorphicto Z_n. Writing shortly cl(x) + isl(x) = z(x),the elements of Γ_n are just the solutions to the equation r(z(x)) = z(nx) = 1.

3 Extending Q(i)

The extension field L_n= Q(i)(Γ_n) is Galois over Q(i). Certainly, Γ_n is finite and so, L_n is algebraic and finite dimensional. As Q(i) has characteristic 0, L_n is separable. Also, if σ is a Q(i)-automorphism of C and γ_k= α_k+ iβ_k ∈ Γ_n, then r(σ(α_k) + iσ(β_k)) = σ(r(α_k + iβ_k)) = 1.Therefore, the equivalence relation

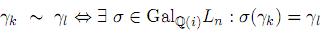
partitions Γ_n into classes of elements sharing the same irreducible polynomial over Q(i). Since L_n is the splitting field of the product of these polynomials, it is normal.

Furthermore, the Galois group Gal_Q(i)L_n= G_n is isomorphic to a subgroup of the multiplicative group U_n of units of Z_n.Actually, the action of G_n on Γ_n defined by σ(γ_k) is a bijection for each fixed σ, which preserves the group structure on Γ_n. That is, there is a group homomorphism Gn →Aut(Γ_n) ≅ Aut(Zn) ≅ Un. Since L_n isalgebraic, this homomorphism is onto.

Now, the order of Un equals the value of Euler's φ-function at n. Thus, if n=2^kp₁p₂··· p_t with different Fermat primes p_i, 1 ≦ i ≦ t, a simple number-theory calculation shows the order of U_n is a power of two. As a result of Lagrange's theorem and basic Galois theory, [L_n: Q(i)] is also a power of two. Hence, the elements of Γ_nare constructible. A convenient reference for this material is the fifteenth chapter of Hungerford's book [5]. So, we have proved Abel's theorem: if n has the given form, then the lemniscate can be split into n equal parts with ruler and compass.

4 Converse

We must elucidate the field structure of L_n. To begin, let us consider the orbits [k] of the action U_n × Z_n → Z_n, (u, k) 7 → uk. We claim that γ_k ∼ γ_l ⇔ [k] = [l]. The implication "⇒" has been already proved: if γ_k ∼ γ_l, there is a u ∈ U_n such that l = uk, i.e., [k] = [l]. The "⇐" part is more elaborate and relies on a careful scrutiny of the general addition formulas for sl(nx), cl(nx). We notice that, when n is odd (respectively, even), the factors cl(x), sl(x) yield the solution γ₀ = 1 (respectively, solutions γ₀= 1, γ_n/₂= −1) of equation r(z(x)) = cl(nx) + isl(nx) = 1 + 0i. Since the remaining factors depend on sl²(x), the elements of Γ_noccur in conjugate pairs within the same equivalence class.

Let us resume the proof where we left off. If [k] = [l], then there is a u ∈ U_n such that l = uk. The case u = 1 is evident. If u = n − 1, γ_l is the complex conjugate 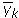of γ_k. The remaining case is when u ∈ U_n \ {1, n − 1}. In this case, the real and imaginary parts of

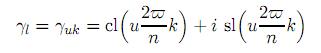
are, via the addition formulas, rational expressions of cl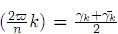 and sl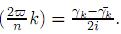. In this way, given u ∈ U_n, there is a permutation γ_j → γ_uj of the equivalence class [γ_k] of γ_k. For, γ_uj is obtained from [γ_k] and Q(i) by a finite sequence of field operations.In other words, it belongs to the splitting field Q(i) ([γ_k]) of the irreducible polynomial associated with [γ_k]. Then, the permutation induces a linear automorphism of Q(i)([γ_k]) which leaves each element of Q(i) unchanged. By performing the process in the other equivalence classes in Γ_n, this automorphism extends in turn to a σ_u ∈ G_n. As σ_u (γ_k) = γ_l, we get γ_k ∼ γ_l.

Consequently, G_n is isomorphic to U_n. Then, [L_n: Q(i)] = φ(n). If the division of the lemniscate into n equal arcs can be constructed, φ(n) is a power of two. By elementary arguments in number theory we conclude that n = 2^kp₁p₂···p_t, where the 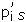are distinct Fermat primes. Theorem1.1 follows.

5 Conclusions

The plainness of the procedure reveals what might be needed for a closed curve to split like the circle or the lemniscate. First, its arc length should be given by an elliptic integral, say 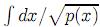for a certain polynomial p. Second, the locus of the solution to Euler's pproblem

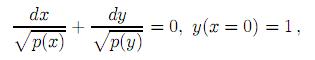
should conveniently match the curve. Third, there should be a periodic parametrization x(t), y(t) of the solution locus such that x(nt), y(nt), n ∈ Z+, are rational functions of x(t), y(t) with rational coefficients. Fourth, the problem should reduce to the constructibility of x((2ϖ /n)k) + iy((2ϖ/n)k), k = 0, 1, . . . , n − 1, where 2ϖ denotes the parametrization period. Fifth, these numbers should be the zeros of equation x(nt) + iy(nt) = 1, etc. For background material on elliptic integrals the reader can consult McKean and Moll [6, chapter 2]. See also [7].

Acknowledgements

This paper has been partially supported by the Vicerrectoría de Investigaciones of Universidad de Medellín and the Facultad de Ciencias of Universidad del Tolima. The authors also wish to thank the referees for their valuable suggestions and improvements in the paper.

References

1. CF. Gauss. Disquisitiones Arithmeticæ, ISBN 958-92-05-15-1. Spanish translation by H. Barrantes, M. Josephy and A. Ruiz, Academia Colombiana de Ciencias Exactas, Físicas y Naturales, Bogotá, 1995. Originally published by Gerh. Fleischer, Leipzig, 1801. Referenciado en 44 [ Links ]

2. NH. Abel. Recherches sur les fonctions elliptiques,ŒuvresComplètes,Christiania (Oslo), 1881. Originally published in Journal fu¨r die reine und angewandte Mathematik, herausgegeben von Crelle, Bd. 2, 3; Berlin, 1827, 1828. Referenciado en 44 [ Links ]

3. Michael Rosen. Abel'sTheoremon the Lemniscate. The American Mathematical Monthly, ISSN 0002-9890, 88(6), 387-395 (1981). Referenciado en 44 [ Links ]

4. U. Hernández, OJ. Palacio. División de la lemniscata: geometría, análisis, álgebra. Facultad de Ciencias, Universidad del Tolima, traba jo de grado del Programa de Matemáticas con énfasis en Estadística, Ibagué-Colombia, 2009. Referenciado en 44 [ Links ]

5. Thomas W. Hungerford. Abstract Algebra, an Introduction, ISBN 0-03-010559- 5. Brooks/Cole, New York, 1996. Referenciado en 47 [ Links ]

6. Henry McKean and Victor Moll. Elliptic Curves: Function Theory, Geometry, Arithmetic, ISBN 978-0521658171. Cambridge University Press, Cambridge, 1999. Referenciado en 48 [ Links ]

7. R. Sridharan. From Lintearia to Lemniscate II: Gauss and Landen's Work . Resonance, ISSN 0971-8044, 9(6), 11-20 (June 2004). Referenciado en 48 [ Links ]