Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
Ingeniería y Ciencia
versão impressa ISSN 1794-9165
ing.cienc. vol.9 no.17 Medellín jan./jun. 2013
ARTÍCULO ORIGINAL
A Remark on the Heat Equation and Minimal Morse Functions on Tori and Spheres
Una nota acerca de la ecuación del calor y funciones de Morse minimales en toros y esferas
Carlos Cadavid Moreno1 and Juan Diego Vélez Caicedo2
1 Ph.D. in mathematics, ccadavid@eafit.edu.co, Universidad EAFIT, Medellín, Colombia.
2 Ph.D. in mathematics, jdvelez@unal.edu.co, Universidad Nacional de Colombia, Medellín, Colombia.
Received: 09-08-2012, Accepted: 24-01-2013
Available online: 22-03-2013
MSC:53C, 53A
Abstract
Let (M, g) be a compact, connected riemannian manifold that is homogeneous, i.e. each pair of points p, q  M have isometric neighborhoods. This paper is a first step towards an understanding of the extent to which it is true that for each ''generic'' initial condition f0, the solution to
M have isometric neighborhoods. This paper is a first step towards an understanding of the extent to which it is true that for each ''generic'' initial condition f0, the solution to  f /
f / t = Δgf, f (
t = Δgf, f ( , 0) = f0 is such that for sufficiently large t, f(
, 0) = f0 is such that for sufficiently large t, f( , t) is a minimal Morse function, i.e., a Morse function whose total number of critical points is the minimal possible on M. In this paper we show that this is true for flat tori and round spheres in all dimensions.
, t) is a minimal Morse function, i.e., a Morse function whose total number of critical points is the minimal possible on M. In this paper we show that this is true for flat tori and round spheres in all dimensions.
Key words: morse function, heat equation.
Highlights
• A novel manifestation of the role played by the heat equation in mathematics is pointed out. • On some homogeneous riemannian manifolds, evolution by the heat equation ''discovers all by itself'' minimal Morse functions.
Resumen
Sea (M, g) una variedad riemanniana que es compacta, conexa y homogénea, es decir, tal que cada par de puntos p, q  M tienen vecindades isométricas. Este artículo constituye un primer paso en el estudio de qué tan general es el hecho de que para cada condición inicial ''genérica'' f0 en (M, g), la solución de
M tienen vecindades isométricas. Este artículo constituye un primer paso en el estudio de qué tan general es el hecho de que para cada condición inicial ''genérica'' f0 en (M, g), la solución de  f /
f / t = Δgf, f (
t = Δgf, f ( , 0) = f0 es tal que para t suficientemente grande, f(
, 0) = f0 es tal que para t suficientemente grande, f( , t) es una función de Morse minimal, es decir, una función de Morse cuyo número total de puntos críticos es el mínimo posible en M. En este artículo se muestra que esto es cierto en el caso de toros planos y esferas redondas, de todas las dimensiones.
, t) es una función de Morse minimal, es decir, una función de Morse cuyo número total de puntos críticos es el mínimo posible en M. En este artículo se muestra que esto es cierto en el caso de toros planos y esferas redondas, de todas las dimensiones.
Palabras clave: función de morse, ecuación del calor.
1 Introduction
The Heat Equation is arguably the most important partial differential equation in mathematics and physics. This equation also seems to be ubiquitous in geometry as well as in many other branches of mathematics. In a suggestive article Serge Lang and Jay Jorgenson called the Heat Kernel ''... a universal gadget which is a dominant factor practically everywhere in mathematics, also in physics, and has very simple and powerful properties''. In this short note we present evidence corroborating the relevance of the Heat Equation, in a seemingly novel direction. Specifically, we present two concrete cases in which the Heat Equation ''discovers all by itself'' minimal Morse functions. This could be, however, a manifestation of a phenomenon that might hold on more general homogeneous riemannian manifolds.
Let M be a closed, connected, oriented smooth manifold, and let g be a riemannian metric on M. On each tangent space Tp(M), the metric g determines a bilinear function {,}g. For any given smooth function f on M, let us recall that the gradient is defined as the vector field grad(f) in T (M) that satisfies {grad(f), ζ}g= ζ(f), for all ζ  T(M). Let us denote by
T(M). Let us denote by  the Levi-Civita connection determined by the metric g. For each smooth vector field X on M, its divergence is defined as div(X) = trace(ζ
the Levi-Civita connection determined by the metric g. For each smooth vector field X on M, its divergence is defined as div(X) = trace(ζ 
 ζ(X)). The Laplacian (or Laplace-Beltrami operator) on (M, g) of a smooth function f : M
ζ(X)). The Laplacian (or Laplace-Beltrami operator) on (M, g) of a smooth function f : M 
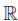 is defined as Δgf = div(grad(f)).
is defined as Δgf = div(grad(f)).
The Heat Equation on (M, g) is the partial differential equation  f /
f / t = Δgf. A solution to the initial condition problem
t = Δgf. A solution to the initial condition problem
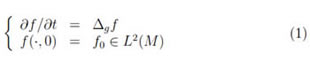
is a continuos function f : M x (0, ∞) 
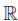 such that
such that
1. For each fixed t > 0, f ( , t) is C2 function, and for each x
, t) is C2 function, and for each x  M, f (x,
M, f (x,  ) is C1.
) is C1.
2.  f /
f / t = Δgf, and
t = Δgf, and
for all ψ  C∞(M).
C∞(M).
It is a non trivial fact that for each t > 0, ft= f( , t) is smooth It is well known that the solution to problem can be obtained in the following way. First, it can be seen that the eigenvalues of the operator Δg, understood as those λ
, t) is smooth It is well known that the solution to problem can be obtained in the following way. First, it can be seen that the eigenvalues of the operator Δg, understood as those λ 
 for which Δgf +λf = 0 for some smooth function f nonidentically zero, are nonnegative and form a discrete set λ0= 0 < λ1<
for which Δgf +λf = 0 for some smooth function f nonidentically zero, are nonnegative and form a discrete set λ0= 0 < λ1< 

 < λj<
< λj< 

 . Moreover, for each j ≥ 0, the corresponding eigenspace Ej has finite dimension mjand Ej
. Moreover, for each j ≥ 0, the corresponding eigenspace Ej has finite dimension mjand Ej  C∞(M). By the assumptions about M, E0 is the one dimensional vector space of constants functions. For each j ≥ 0 let Bj = {φj,i: i = 1, ..., mj} be an orthonormal basis for Ej. Their union B =
C∞(M). By the assumptions about M, E0 is the one dimensional vector space of constants functions. For each j ≥ 0 let Bj = {φj,i: i = 1, ..., mj} be an orthonormal basis for Ej. Their union B = 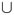 Bj is an orthonormal basis for L2(M). Then, the solution to problem can be written as
Bj is an orthonormal basis for L2(M). Then, the solution to problem can be written as
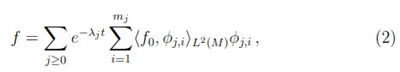
where {-, -}L2(M) denotes the inner product of L2(M).
We want to address the following question: to what extent is it true that for each ''generic'' initial condition f0, the solution to is such that for sufficiently large t, ft is a minimal Morse function, i.e., a Morse function whose total number of critical points is less or than equal to that of any other Morse function on M? Below, we show that the answer to this question is affirmative for flat tori and round spheres. A key ingredient in the proof is the following result which is a corollary of Mather's Stability Theorem [4].
Theorem 1.1 (Stability of Morse functions). Let M de a smooth manifold and let h : M  R be any Morse function. Then, there exists an open neighborhood Wh in the C∞ topology (of C∞(M)) such that any function φ
R be any Morse function. Then, there exists an open neighborhood Wh in the C∞ topology (of C∞(M)) such that any function φ  Wh is Morse with the same number of critical points as h. When M is compact, the C∞ topology (of C∞(M)) is the union of all Crtopologies (of C∞(M)) so in this case the conclusion can be restated as follows: There exists r > 0 and > 0 such that, if
Wh is Morse with the same number of critical points as h. When M is compact, the C∞ topology (of C∞(M)) is the union of all Crtopologies (of C∞(M)) so in this case the conclusion can be restated as follows: There exists r > 0 and > 0 such that, if  φ - h
φ - h  r< for φ
r< for φ  C∞(M) and
C∞(M) and 

 being the Cr-norm, then φ is also a Morse function with the same number of critical points as h.
being the Cr-norm, then φ is also a Morse function with the same number of critical points as h.
2 Tori
Let Tn denote the n-dimensional flat torus obtained as the quotient of 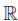 n by the obvious action of (2π
n by the obvious action of (2π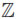 )n by isometries. In this case the spectrum of the Laplacian is the set {λj: j ≥ 0} where λj is the j-th integer that can be written as a sum of squares
)n by isometries. In this case the spectrum of the Laplacian is the set {λj: j ≥ 0} where λj is the j-th integer that can be written as a sum of squares 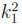 +
+

 +
+ 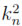 for some nonnegative integers k1, . . . , kn [6] Notice that λ0= 0 (as it should) and λ1= 1. An orthonormal basis Bj for Ej is given by the functions in Tninduced by the functions in
for some nonnegative integers k1, . . . , kn [6] Notice that λ0= 0 (as it should) and λ1= 1. An orthonormal basis Bj for Ej is given by the functions in Tninduced by the functions in  n of the form
n of the form
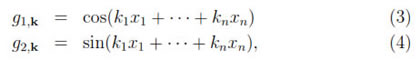
where k denotes a n-tuple (k1, . . . kn), such that 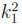 +
+

 +
+ 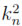 =λj. The set B =
=λj. The set B = 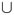 j≥0Bj is an orthonormal basis of L2(Tn). In particular, B1 is {cos(x1), sin(x1), . . . , cos(xn), sin(xn)}.
j≥0Bj is an orthonormal basis of L2(Tn). In particular, B1 is {cos(x1), sin(x1), . . . , cos(xn), sin(xn)}.
Lemma 1. The function induced on Tn by h = 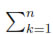 (ak cos(xk) + bk sin(xk)) is a Morse function, if and only if,
(ak cos(xk) + bk sin(xk)) is a Morse function, if and only if, 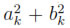
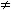 0 for every k. Moreover, if it is Morse it is a minimal Morse function.
0 for every k. Moreover, if it is Morse it is a minimal Morse function.
Proof. First, we observe that a smooth function on Tn is Morse if and only if its pullback is Morse. Now, each partial derivative  h/
h/ xk= -ak sin(xk) + bk cos(xk) can be rewritten in the form Ak sin(xk+ θk) = 0, where Ak=
xk= -ak sin(xk) + bk cos(xk) can be rewritten in the form Ak sin(xk+ θk) = 0, where Ak= 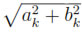 ,and the θk are suitable constants. We notice that h is Morse if and only if whenever (x) = (x1, . . . , xn)
,and the θk are suitable constants. We notice that h is Morse if and only if whenever (x) = (x1, . . . , xn) 
 n is a solution to the system Ak sin(xk+ θk) = 0, k = 1, . . . , n, (x) is not a zero of the the determinant of the Hessian matrix, which can be readily computed as
n is a solution to the system Ak sin(xk+ θk) = 0, k = 1, . . . , n, (x) is not a zero of the the determinant of the Hessian matrix, which can be readily computed as
det Hess(h) = (-1)n(a1cos(x1) + b1 sin(x1)) 

 (ancos(xn) + bn sin(xn)) .
(ancos(xn) + bn sin(xn)) .
It is easy to see that this is the case if and only if 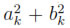
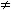 0, for each k = 1, . . . , n. On the other hand, it is a general fact that the sum of the betti numbers of a manifold M is a lower bound for the number of critical points of any Morse function on M. Using Künneth's formula we see that the sum of the betti numbers of Tn equals 2n. Finally, the system Ak sin(xk+ θk) = 0, k = 1, . . . , n, under the assumption that
0, for each k = 1, . . . , n. On the other hand, it is a general fact that the sum of the betti numbers of a manifold M is a lower bound for the number of critical points of any Morse function on M. Using Künneth's formula we see that the sum of the betti numbers of Tn equals 2n. Finally, the system Ak sin(xk+ θk) = 0, k = 1, . . . , n, under the assumption that 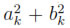
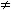 0, for all k, has 2n solutions in the box [0, 2π)n. This allows us to conclude that h is a minimal Morse function.
0, for all k, has 2n solutions in the box [0, 2π)n. This allows us to conclude that h is a minimal Morse function.

Theorem 2.1. There exists a set S 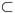 C∞ (Tn), that is dense and open in the C∞ topology, such that for any initial condition f0
C∞ (Tn), that is dense and open in the C∞ topology, such that for any initial condition f0 S, if f is corresponding solution to then there exists T > 0, depending on f0, so that for each t ≥ T, the function ft= f(
S, if f is corresponding solution to then there exists T > 0, depending on f0, so that for each t ≥ T, the function ft= f( , t) is minimal Morse.
, t) is minimal Morse.
Proof. Let f0= h0+ h1+ 

 where each hj is the projection of f0 on Ej. Let us fix a nonnegative integer r, and let
where each hj is the projection of f0 on Ej. Let us fix a nonnegative integer r, and let 

 r be the Cr norm on C∞(M) (see [5]). As noticed in the introduction, ft=
r be the Cr norm on C∞(M) (see [5]). As noticed in the introduction, ft= 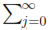 = e-λjthj. In order to prove that ftis minimal Morse for all t sufficiently large, it suffices to show that the same is true for eλ1t(ft- h0). We have
= e-λjthj. In order to prove that ftis minimal Morse for all t sufficiently large, it suffices to show that the same is true for eλ1t(ft- h0). We have
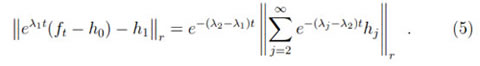
Now we show that the second factor in the right hand side of is bounded on Tn x [1, ∞). Let us write hj = ∑k(cj,kg1,k + dj,kg2,k), where the g1,k and g2,k are as in (3). It can be seen inductively that for i = 1, 2, then  gi,k/
gi,k/ xis
xis 


 xi1 is equal to ± ki1
xi1 is equal to ± ki1 

 kisgl,k, for some l = 1, 2. Using these we can estimate the sum in (5) as follows:
kisgl,k, for some l = 1, 2. Using these we can estimate the sum in (5) as follows:
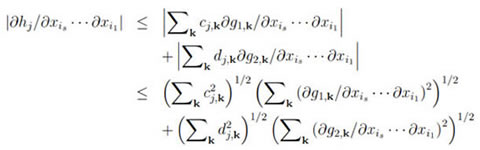
by the Cauchy-Schwartz inequality.
Since  gi,k/
gi,k/ xis
xis 


 xi1 =±ki1
xi1 =±ki1 

 kisgl,k, for some l = 1, 2. Now, the number of all possible n tuples k = (k1, . . . , kn) such that
kisgl,k, for some l = 1, 2. Now, the number of all possible n tuples k = (k1, . . . , kn) such that 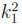 +
+

 +
+ 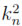 = λj is clearly bounded above by
= λj is clearly bounded above by 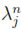 . Thus,
. Thus,
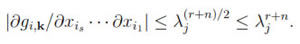
Hence,
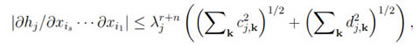
and consequently, 
 hj/
hj/ xis
xis 


 xi1
xi1  ≤
≤ 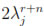
 f0
f0 L2(Tn).It follows immediately that
L2(Tn).It follows immediately that  hj
hj r≤
r≤ 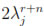
 f0
f0 L2(Tn). From this we get the estimate
L2(Tn). From this we get the estimate
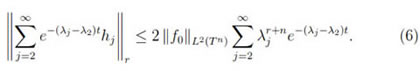
It is to verify the convergence of the series on the right hand side of for each fixed value of t ≥ 1. Since the sum of this series decreases as t increases, we deduce that 
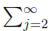 e-(λj-λ2)t hj
e-(λj-λ2)t hj r is bounded on Tn x [1, ∞). Finally, this implies that
r is bounded on Tn x [1, ∞). Finally, this implies that
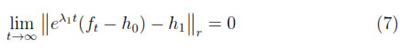
for each r ≥ 0.
Let us assume that h1is a minimal Morse function. By Theorem 1.1 there exist r = r(h1) > 0 and = (h1) > 0 such that every φ  C∞(M) with
C∞(M) with  φ - h1
φ - h1 r <
r <  0 is Morse and has the same number of critical points as h1. Since limt
0 is Morse and has the same number of critical points as h1. Since limt ∞
∞  eλ1t(ft- h0) - h1
eλ1t(ft- h0) - h1 r= 0, there is a T0> 0 such that if t ≥ T0,
r= 0, there is a T0> 0 such that if t ≥ T0,
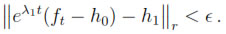
This implies that if t ≥ T0, the function eλ1t(ft- h0) - h1 is Morse and has the same number of critical points as h1. This allows us to conclude that for t ≥ T0, eλ1t(ft- h0) - h1 is minimal Morse, and so it is ft. The proof is finished by verifying that the subset S  C∞(Tn) of all functions whose projection on E1 is minimal Morse is open and dense in the C∞ topology. Since the C0 norm bounds from above the L2 norm (Tn is compact), then two functions close in the C0 sense are also close in the L2 sense and therefore the coefficients in their Fourier expansions are also close. A combination of this with Lemma shows that a smooth function that is close to a smooth function whose projection on E1 is minimal Morse, must also have projection on E1 that is minimal Morse. Finally, let us show that S is dense in C∞(Tn). It suffices to prove that for any smooth f0= h0+ h1 +
C∞(Tn) of all functions whose projection on E1 is minimal Morse is open and dense in the C∞ topology. Since the C0 norm bounds from above the L2 norm (Tn is compact), then two functions close in the C0 sense are also close in the L2 sense and therefore the coefficients in their Fourier expansions are also close. A combination of this with Lemma shows that a smooth function that is close to a smooth function whose projection on E1 is minimal Morse, must also have projection on E1 that is minimal Morse. Finally, let us show that S is dense in C∞(Tn). It suffices to prove that for any smooth f0= h0+ h1 + 

 , r > 0, and
, r > 0, and  > 0, there is
> 0, there is 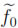
 S such that
S such that  f0-
f0- 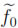
 r <
r <  . It is enough to define
. It is enough to define 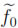 with the same Fourier expansion as f0 except that h1 is replaced by a minimal Morse function
with the same Fourier expansion as f0 except that h1 is replaced by a minimal Morse function 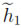 , such that
, such that  h1-
h1- 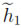
 r <
r <  .
.

3 Spheres
In this section with prove a result similar to Theorem 2.3 for the n-dimensional sphere Sn = {(x1, . . . , xn +1) : 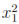 +
+

 +
+ 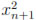 = 1}
= 1} 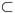
 n+1, n ≥ 1, with the metric induced from
n+1, n ≥ 1, with the metric induced from  n+1. In this case, it is well known that the eigenvalues of the Laplacian operator are given by λj = j(j + n - 1), j ≥ 0 and the corresponding eigenfunctions, the so called spherical harmonics, are given as the restriction to the sphere of homogeneous polynomials H(x1, . . . , xn+1)in the coordinates of
n+1. In this case, it is well known that the eigenvalues of the Laplacian operator are given by λj = j(j + n - 1), j ≥ 0 and the corresponding eigenfunctions, the so called spherical harmonics, are given as the restriction to the sphere of homogeneous polynomials H(x1, . . . , xn+1)in the coordinates of  n+1,of total degree j, which satisfy the condition
n+1,of total degree j, which satisfy the condition
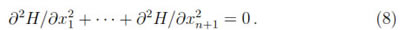
The corresponding eigenspace of λj, Ej, turns out to be a space of dimension 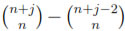 [7]. (In the latter formula it is understood that
[7]. (In the latter formula it is understood that 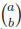 = 0 in case a < b.) When j = 1, λ1= n, and a basis for E1 is given by the n + 1 coordinate functions x1, . . . , xn+1. Each nonzero linear form in these variables is a Morse function with two critical points, which is the minimal possible, since this is precisely the sum of the betti numbers of Sn.
= 0 in case a < b.) When j = 1, λ1= n, and a basis for E1 is given by the n + 1 coordinate functions x1, . . . , xn+1. Each nonzero linear form in these variables is a Morse function with two critical points, which is the minimal possible, since this is precisely the sum of the betti numbers of Sn.
Moreover, if h denotes the restriction of a harmonic homogeneous polynomial H to Sn, the following estimate holds for the sup norm (C0-norm in M):
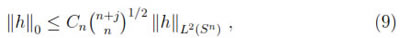
where Cn is a constant that only depends on n ([7] Section 7). Moreover, in the Cr-norm on Sn, the following more general estimate holds ([8])
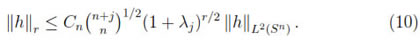
With these preliminaries we can state the following theorem.
Theorem 3.1. There exists a set S 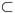 C∞(Sn), that is dense and open in the C∞ topology, such that for any initial condition f0
C∞(Sn), that is dense and open in the C∞ topology, such that for any initial condition f0 S, if f is corresponding solution to (1), then there exists T > 0, depending on f0, so that for each t ≥ T , the function ft= f(
S, if f is corresponding solution to (1), then there exists T > 0, depending on f0, so that for each t ≥ T , the function ft= f( , t) is minimal Morse.
, t) is minimal Morse.
Proof. Let f0= h0+ h1+ This implies that Hence, where K0= 4 Conclusions In this article a novel manifestation of the role played by the heat equation in mathematics is pointed out; namely, that in some homogeneous riemannian manifolds, evolution by the heat equation of a generic initial datum ''discovers all by itself'' a minimal Morse function for the manifold, i.e. one whose total number of critical points is less than or equal to that of any other Morse function admitted by the manifold. In the future the authors intend to verify whether the same phenomenon takes place on other families of homogeneous riemannian manifolds. Aknowledgements We thank the Universidad Nacional of Colombia and Universidad EAFIT for their invaluable support. References [1] L. Serge and J. Jorgenson, The ubiquitous heat kernel.Mathematics Unlimited-'' 2001 and Beyond. Berlin: Springer, 2001. [ Links ] 12 [2] I. Chavel, Eigenvalues in Riemannian Geometry. Academic Press Inc., 1984. [ Links ] 13 [3] S. Rosenberg, The Laplacian on a Riemannian Manifold: An Introduction to Analysis on Manifolds. London: London Mathematical Society Student Texts 31, 1997. [ Links ] 13 [4] J. Mather, ''Stability of C infinite mappings implies Stability,'' Annals of Mathematics, vol. 89, no. 2, pp. 254-291, 1969. [ Links ] 14 · · where each hjis the projection of f0 on Ej, and let ft denote the solution to the Heat Equation with initial condition f0. In order to prove that ft is minimal Morse for all t sufficiently large, it suffices to show that the same is true for eλ1t(ft- h0). Let us fix a positive integer r. As in the previous proof, the key issue is to show that
· · where each hjis the projection of f0 on Ej, and let ft denote the solution to the Heat Equation with initial condition f0. In order to prove that ft is minimal Morse for all t sufficiently large, it suffices to show that the same is true for eλ1t(ft- h0). Let us fix a positive integer r. As in the previous proof, the key issue is to show that 
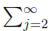 e-(λj-λ2)thj
e-(λj-λ2)thj r is bounded on Sn x [1, ∞). Let us notice that λj- λ2 = j(j + n - 1) - 2(n + 1) becomes greater that n + j for any j sufficiently large. On the other hand, ex is also greater than x2
r is bounded on Sn x [1, ∞). Let us notice that λj- λ2 = j(j + n - 1) - 2(n + 1) becomes greater that n + j for any j sufficiently large. On the other hand, ex is also greater than x2 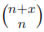 (1 + x)r for all x ≥ N. Thus, for all j ≥ Nt ≥ N, and t ≥ 1
(1 + x)r for all x ≥ N. Thus, for all j ≥ Nt ≥ N, and t ≥ 1 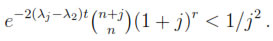
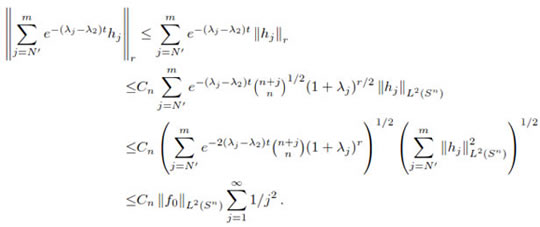
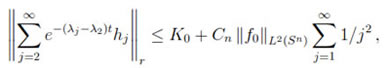
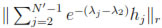 , which proves the claim. The rest of the proof is exactly as that of the theorem above.
, which proves the claim. The rest of the proof is exactly as that of the theorem above.
[5] H. Morris, Differential Topology. Springer-Verlag, 1976. [ Links ] 14, 15
[6] L. Grafakos, Classical Fourier Analysis. Springer Science, 2nd ed., 2008. [ Links ] 14
[7] P. Garret, ''Harmonic Analysis on Spheres I.'' 2010. [ Links ] 18
[8] P. Garret, ''Harmonic Analysis on Spheres II.'' 2011. [ Links ] 18













