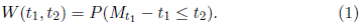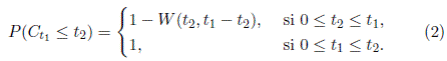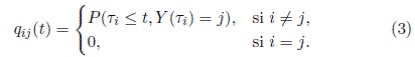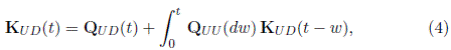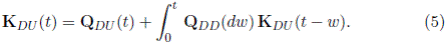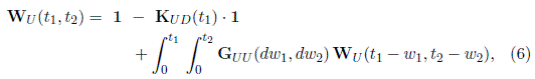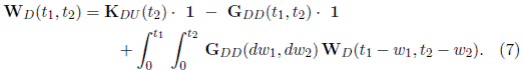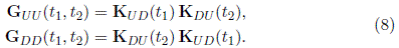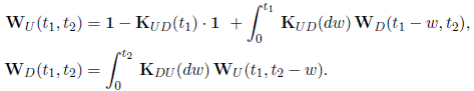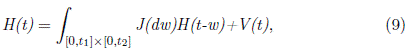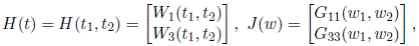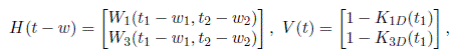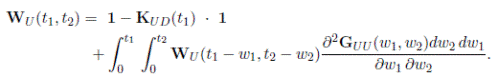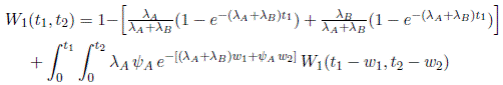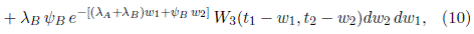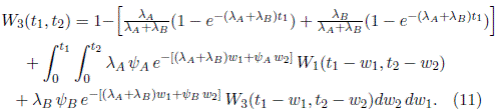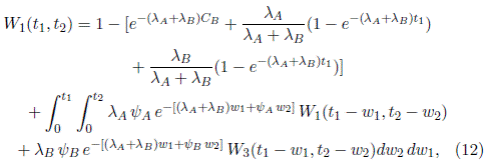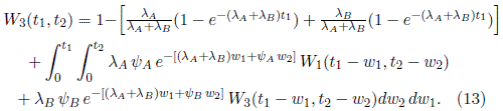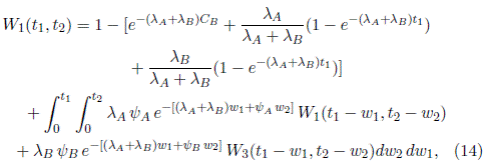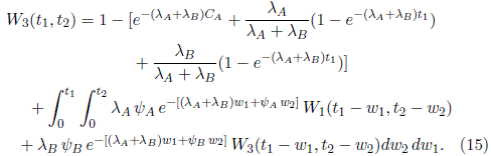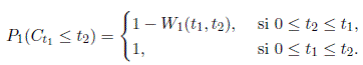1 Introducción
Las estructuras reparables en ingeniería han sido motivo de muchas investigaciones, debido a que es necesario evidenciar el buen funcionamiento de los distintos mecanismos, su tolerancia a fallos, que se incluye en sus componentes, y, como resultado, poder dar cierta confianza en el servicio que proporcionan. Guo et al. [1] proponen un nuevo modelo de reparación general, basado en el historial de reparaciones, y Yi et al. [2] presentan sistemas en series reparables utilizando el método de matriz, que ha sido ampliamente utilizado en procesos estocásticos agregados, especialmente, en modelado de canales iónicos y sistemas reparables agregados; las fórmulas de fiabilidad, disponibilidad instantánea e intervalo se dan en matrices.
El análisis de estructuras reparables, desde el punto de vista probabilístico, se encarga de las características operativas mediante modelos estocásticos adecuados; es así como se encuentran los campos de la fiabilidad y la disponibilidad, para evaluar estos se utilizan diferentes técnicas de modelado, dependiendo de las suposiciones de operación del sistema (degradación y reparación). Kayedpour et al. [3] desarrollan un algoritmo integrado para resolver el problema de diseño de fiabilidad, considerando la disponibilidad instantánea, componentes reparables y la selección de estrategias de configuración, basadas en los procesos de Markov y el algoritmo NSGA-II. Melo et al. [4] presentan la estimación de la confiabilidad-dis ponibilidadmantenibilidad, mediante una simulación tipo Monte Carlo de un sistema de compresión de gas amargo de una plataforma costa afuera, durante la etapa de ingeniería, a partir de las tasas de fallas de los equipos mecánicos e instrumentos.
Dentro del campo de la fiabilidad se estudia la estimación de la proporción del tiempo operativo de la estructura; es decir, de la proporción de tiempo en el cual la estructura realmente está trabajando durante un intervalo dado de tiempo; se puede hacer a referencia los trabajos de: Navas [5], quien plantea cómo la intensidad de fallo de un elemento reparable se puede estimar empleando los tiempos sucesivos entre fallos, mediante un Proceso Puntual Estocástico. Si los tiempos entre fallos se distribuyen exponencialmente, entonces la intensidad de fallo es constante y se puede modelar por un Proceso de Poisson Homogéneo. En los casos en los que no existe una tendencia en la intensidad de fallo, puede ser de aplicación el Proceso de Poisson No Homogéneo. Ardakan et al. [6] muestran que la fiabilidad de los componentes se considera como una función del tiempo, y el RAP ( Redundancy allocation problem ) se reformula mediante la introducción de un nuevo criterio llamado:“mission design life", definida como la integración de la función de confiabilidad del sistema durante el tiempo de la misión. López [7] presenta un nuevo proceso estocástico, denominado proceso potencial, que permite modelar los tiempos de operatividad y de reparación en un sistema en deterioro, en el que involucra el concepto de reparación pospuesta.
Una medida para evaluar la estructura en cuanto a su rendimiento es mediante su disponibilidad, y esta depende de la distribución del tiempo de vida útil de cada una de las unidades de la estructura y de la capacidad de recuperación de la misma. Muchos autores han hecho un aporte científico al concepto de disponibilidad, entre muchos investigadores se puede mencionar a: Csenki [8], quien da a conocer su trabajo intitulado: Disponibilidad conjunta de los sistemas modelados por procesos semimarkovianos finitos. Posteriormente, presenta sus trabajos: Disponibilidad de misión de sistemas de Markov semi-reparable [9], análisis transitorio de la disponibilidad de intervalo para sistemas reparables modelados por procesos semimarkovianos finitos [10]. Entre tanto, Donaticllo y Lyer [11], muestran una solución de forma cerrada para la distribución de la disponibilidad del sistema. Rubino y Sericola [12] exponen sus ideas sobre el intervalo de cálculo de distribución de la disponibilidad.
Aportes recientes sobre disponibilidad son los hechos por Alaswad y Xiang [13], quienes muestran una revisión de la literatura CBM (Conditionbased maintenance) con énfasis en modelos matemáticos y enfoques de optimización; Arunachalam et al. [14] presentan la función de disponibilidad en términos de una ecuación integral y muestran, a la vez, posibles soluciones; Bednara [15] presenta los métodos existentes para calcular la función de disponibilidad; Calvache [16] comparte su trabajo sobre aproximaciones de las funciones de renovación y de disponibilidad, con aplicaciones en el área administrativa. Calvache [17] expone la obtención de los momentos transitorios y estables del tiempo de misión de la disponibilidad del sistema sujeto a fallas, así como el análisis de su función de distribución, mediante el uso de la teoría de las distribuciones de tiempo de viaje de un móvil, que transita por un número finito de caminos, en los que la velocidad promedio del móvil varía de camino a camino. Cui et al. [18] presentan dos nuevos índices de disponibilidad de intervalos para sistemas reparables de Markov; Donatiello e Iyer [11] reporta una solución de transformación de Laplace para la distribución de disponibilidad en un intervalo finito, para un modelo semi-Markov. La transformación de la distribución se invierte analíticamente para obtener una solución de forma cerrada para el modelo de Markov correspondiente; Rubino y Sericola [12] consideran un sistema informático reparable con dos estados, primero tratan con procesos semi-Markov, y bajo algunas condiciones desarrollan un método para calcular la distribución de disponibilidad; Sericola [19] define un nuevo algoritmo para calcular la distribución de disponibilidad de intervalos para sistemas que tienen un solo estado operativo. Existen artículos en los que se han estudiado estructuras reparables dispuestas en paralelo, como se puede observar en Hu et al. [20], quienes estudian la equivalencia de disponibilidad de diferentes diseños de un sistema en serie paralelo reparable, bajo el supuesto de que los componentes del sistema tienen tasas de falla y reparación constantes; Csenki [21] presenta una nueva aproximación del tiempo operacional acumulativo para modelos de sistemas reparables, y El-Damcese et al. [22] analizan un sistema en serie-paralelo mediante el uso del proceso semi-Markov, en donde hay espacio para realizar mantenimiento preventivo al sistema y, así, aumentar la vida útil del sistema; con base en estos dos últimos artículos el aporte de estas líneas es el de desarrollar un estudio detallado de estructuras reparables de dos unidades dispuestas en serie; se modela la disponibilidad mediante un sistema de ecuaciones integrales y se resuelve mediante el uso de algunos métodos numéricos. Estos resultados son muy importantes en el campo de la ingeniería industrial.
Ejemplos clásicos de estructuras en serie son algunos sistemas de tuberías en donde se puede encontrar una tubería de descarga, una válvula, una bomba y una tubería de succión, y es necesario que todas estas componentes estén dispuestas en serie, y en ese orden, para que la estructura funcione; también, se puede encontrar en los microcomponentes de un equipo electrónico transistores que, en muchos casos, requieren estar dispuestos en serie para hacer algún trabajo específico.
2 Descripción del modelo
Para la descripción del modelo se considera una estructura en serie reparable cuyas componentes son dos unidades: A y B, que, en general, presentan diferentes características técnicas. Se asume que cuando una de las unidades falla, inmediatamente, entra a reparación. Igualmente, cuando transcurra un tiempo especificado sin que ninguna unidad falle se hará un mantenimiento preventivo, de manera alternativa; inicialmente, se realiza sobre una unidad; la siguiente ocasión se hará sobre la otra unidad, y así sucesivamente. Una vez se haga reparación o mantenimiento preventivo a una unidad, ésta se considera “en excelentes condiciones para realizar su trabajo". Pero si una unidad fue reparada últimamente, el siguiente mantenimiento preventivo se hará sobre la otra unidad.
Para cada una de las unidades se manejan tres tiempos: de vida (V
i
), reparación (R
i
) y mantenimiento (M
i
), cada uno de ellos es independiente de los otros y con comportamiento exponencial. La simbolización utilizada es: V
i
~ exp(λ
i
),
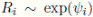 y
y
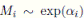 , con i = A, B. Nótese que como las variables aleatorias V
A
y V
B
son continuas, entonces P (V
A
= V
B
) = P ((V
A
, V
B
) = (t, t), para algún t ∈ R) = 0; es decir, en este modelo, la probabilidad de que las dos unidades fallen simultáneamente es cero, por tanto en ningún momento las dos unidades entran a reparación al mismo tiempo.
, con i = A, B. Nótese que como las variables aleatorias V
A
y V
B
son continuas, entonces P (V
A
= V
B
) = P ((V
A
, V
B
) = (t, t), para algún t ∈ R) = 0; es decir, en este modelo, la probabilidad de que las dos unidades fallen simultáneamente es cero, por tanto en ningún momento las dos unidades entran a reparación al mismo tiempo.
Así, el modelo por estudiar será el proceso que describe si la estructura está o no funcionando en un tiempo t, después de haber sido puesta en funcionamiento. Este modelo se denota por Y = {Y (t), t ≥ 0} y es semimarkoviano [8],[9],[10].
A continuación se presentan el espacio de estados S del proceso Y (ver Figura 1], y teniendo en cuenta que cada una de las unidades de la estructura puede estar funcionando o, en caso contrario, estar siendo reparada, o estar en mantenimiento preventivo, constará de seis elementos: S = {1, 2, . . . , 6}. El significado de cada uno de los estados es el siguiente:
Los estados 1 y 3 representan aquellos en los que tanto la unidad A como la unidad B están funcionando. Al estado 1 se accede en el caso en que en el estado anterior del proceso, la unidad A no estuviera funcionando y la unidad B no presentara falla; mientras, al estado 3 se accede en caso de que en el estado anterior, la unidad A estuviera funcionando mientras que la unidad B no.
El estado 2 representa aquel en que la unidad A funciona y la unidad B entra a mantenimiento preventivo.
El estado 4 representa aquel en que la unidad A entra a mantenimiento preventivo y la unidad B funciona.
El estado 5 representa aquel en que la unidad A está en reparación y la unidad B funciona.
El estado 6 representa aquel en que la unidad A funciona y la unidad B está en reparación.
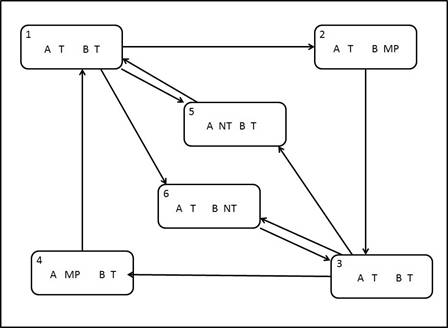
Figura 1: Transiciones del proceso Y = {Y (t), t ≥ 0}; donde A y B son las unidades, T hace referencia que la unidad trabaja, MP hace referencia que la unidad entra a mantenimiento preventivo y NT hace referencia que la unidad está en reparación porque ha presentado alguna falla.
Estos estados pueden subdividirsen en: U = {1, 3} y D = {2, 4, 5, 6}, donde cada uno de los estados del conjunto U, indican que la estructura está en funcionamiento, mientras que los estados del conjunto D, indican lo contrario.
Además, se considera los siguientes supuestos:
La primera unidad en entrar a mantenimiento preventivo es la unidad B, después de estar en funcionamiento la estructura durante un tiempo C B . Si después de haber sido reparada la unidad B ó después de habérsele hecho mantenimiento preventivo, la estructura no falla durante un tiempo C A se realiza mantenimiento preventivo a la unidad A y, de esta manera alternativa, se realizan los siguientes mantenimientos preventivos.
El modelo no contempla el caso en que las dos unidades fallen simultáneamente, debido a que la probabilidad de que las dos unidades fallen al mismo tiempo es cero.
Solo se cuenta con disponibilidad para matenimiento o arreglo de una unidad.
3 Conceptos y resultados básicos
En esta sección se incluye algunas nociones y resultados inherentes al estudio de la disponibilidad de una estructura en serie:
El tiempo de acumulación operativo C t es el tiempo total en el cual el proceso Y permanece en uno de los estados en el que funciona, durante el intervalo de tiempo 0, t. También, {C = C t │ t ≥ 0} es el proceso estocástico de tiempos de acumulación operativo.
M v es el tiempo aleatorio, requerido para que la estructura esté en funcionamiento durante un tiempo predeterminado v. A v se le llama duración de la misión y a M v se le llama tiempo de la misión. También, M = {M v │ v ≥ 0} proceso estocástico de tiempos de misión. Este concepto de tiempo de misión es tratado conceptualmente por Calvache [17] con aplicaciones a un sistema en donde fallan varios de sus componentes.
M v - v es el tiempo total en reparación, asociado con una duración de misión v.
Para t, v ≥ 0:
C t ≥ v ⇔ M v ≤ t.
La disponibilidad del tiempo en una misión (WMA), denotada por W (t 1 , t 2), es la probabilidad de que en total, no haya más de t 2 unidades de tiempo total en reparación, asociada con una duración de misión t 1.
Nótese que si 0 ≤ t 2 ≤ t 1 < ∞,
W (t 2 , t 1 − t 2) = P (M t 2 − t 2 ≤ t 1 − t 2)
= P (M t 2 ≤ t 1)
= P (C t 1 ≥ t 2).
La notación con subíndices en probabilidades se usa para denotar probabilidades con una condición inicial, de la siguiente manera:
P s (A) = P (A | Y (0) = s), para todo s ∈ S y para todo evento A. Por ejemplo: W s (t 1 , t 2) = P (M t 1 − t 1 ≤ t 2 | Y (0) = s).
W(t 1 , t 2) es el vector (W s (t 1 , t 2))s∈S .
Si B = U ó B = D, τ B es el primer tiempo de permanencia de Y en B. Esto es el tiempo gastado por Y en B durante esta primera visita a B. Así que, si Y (0) ∈ U entonces τ U es el lapso del primer período de trabajo, y si Y (0) ∈ D, entonces τ D es el lapso del primer período de reparación. Además, el tiempo de espera o permanencia del proceso en un estado i ∈ B es el tiempo aleatorio τ i , que corresponde al tiempo en que el proceso permanece en el estado i.
En referencia a la tesis de Rodríguez [23] se demuestra que el proceso Y es semi-markoviano, el cual tiene como núcleo a la matriz Q(t), la cual se calcula mediante:
La notación con subíndices en matrices se usa para denotar submatrices o sub-vectores. Por ejemplo: Q D,U (t) = (q d,u ) d∈D,u∈U .
Ahora, el resultado principal para determinar la disponibilidad del tiempo en una misión, el cual será usado en la aplicación de este artículo, es presentado por Csenki [21], quien demostró que en una estructura reparable se satisface el siguiente teorema:
Teorema Central 1. La matriz de valores de las funciones K
UD
(t) y K
DU
(t) sobre
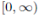 están dadas por:
están dadas por:
Además, si W U (t 1 , t 2) y W D (t 1 , t 2) son vectores cuyas componentes son las disponibilidades de tiempo para una misión cuando la estructura inicia en los diferentes estados de U y D, respectivamente, entonces estos satisfacen las ecuaciones integrales:
donde las funciones G UU y G DD sobre [0, ∞)2 son definidas por:
También, los dos subvectores W U y W D del vector WMA se pueden expresar uno términos del otro, como:
Por otra parte, las ecuaciones dadas en este teorema son casos particulares del sistema:
donde:
los vectores V (t), J (dw) son conocidos y H es desconocido. El sistema dado por (9) es solucionado por Boehme [24], quien lo resuelve mediante un método numérico.
4 Disponibilidad para los estados en funcionamiento
Para encontrar W U (t 1 , t 2) en nuestro modelo se usará la ecuación integral dada en (6) y el resultado (16) y, dado que la función exponencial es derivable, dicha ecuación se puede expresar como:
Las componentes de W U (t 1 , t 2) para el modelo se presenta en tres casos:
Caso 1. Si t 1 < C B y t 2 ≥ 0,
Caso 2. Si C B ≤ t 1 < C A y t 2 ≥ 0,
Caso 3. Si t 1 > C A y t 2 ≥ 0,
Los sistemas de ecuaciones integrales (10) y (11); (12) y (13), y (14) y (15) son casos particulares del sistema (9). Para poder resolver numéricamente este sistema es necesario tomar casos particulares de este modelo y aplicarle el método numérico desarrollado por Boehme [24]. En la siguiente sección se plantearán casos ilustrativos, con su respectiva solución.
5 Ejemplo numérico
Un proceso industrial es comprendido como todo desarrollo sistemático; implica una serie de pasos ordenados y organizados, que suceden de forma alternativa o simultánea, los cuales se encuentran estrechamente relacionados entre sí y cuyo propósito es llegar a un resultado preciso. Una forma de medir este proceso es mediante la función de distribución acumulativa (Cdf) del tiempo operacional acumulativo en un intervalo de tiempo finito
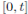 , que se representa en términos de disponibilidad.
, que se representa en términos de disponibilidad.
Como se mencionó anteriormente la disponibilidad del tiempo en una misión (WMA) dada por (1), es la probabilidad de que en total, no haya más de t 2 unidades de tiempo total en reparación asociada con una duración de misión t 1, y su expresión está dada por:
W (t 1 , t 2) = P (M t 1 − t 1 ≤ t 2).
Ahora, fijando un tiempo t
1 y variando un tiempo t
2, se encuentran los sistemas de ecuaciones integrales indicadas en la anterior sección. La solución es dada por (9). Por medio de esta se halla las aproximaciones para
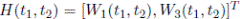 . El objetivo es encontrar la función de distribución de C
t
1 en el caso de que el proceso empiece en el estado 1; es decir, si Y = 1 y para esto se utilizan los resultados de W
1(t
1
, t
2), mediante (2):
. El objetivo es encontrar la función de distribución de C
t
1 en el caso de que el proceso empiece en el estado 1; es decir, si Y = 1 y para esto se utilizan los resultados de W
1(t
1
, t
2), mediante (2):
El ejemplo que, a continuación, se presenta cuenta con dos unidades A y B. Se asume que las dos unidades no presentan ninguna falla; para cada una de las unidades se presentan los tiempos: de vida (V
i
), reparación (R
i
) y mantenimiento (M
i
). Cada uno de ellos es independiente de los otros y con comportamiento exponencial. Los valores supuestos de los parámetros del modelo para la unidad A se dan de la siguiente manera:
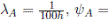
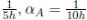 , el tiempo de funcionamiento antes de entrar a mantenimiento preventivo es C
A
= 90h; para la unidad B es:
, el tiempo de funcionamiento antes de entrar a mantenimiento preventivo es C
A
= 90h; para la unidad B es:
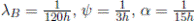 el tiempo de funcionamiento antes de entrar a mantenimiento preventivo, es: C
B
= 65h y un tiempo de misión de la estructura t
m
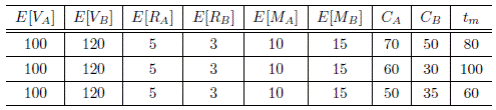
= 120. En la Tabla 1 se muestra los valores esperados de los tiempos de vida, de reparación y mantenimiento, asumidos por el modelo (dados en horas) tanto para la unidad A como para la unidad B.
el tiempo de funcionamiento antes de entrar a mantenimiento preventivo, es: C
B
= 65h y un tiempo de misión de la estructura t
m
= 120. En la Tabla 1 se muestra los valores esperados de los tiempos de vida, de reparación y mantenimiento, asumidos por el modelo (dados en horas) tanto para la unidad A como para la unidad B.
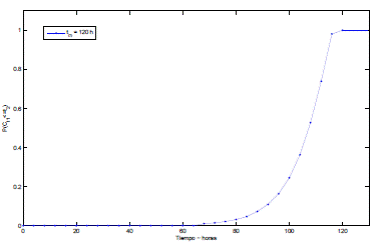
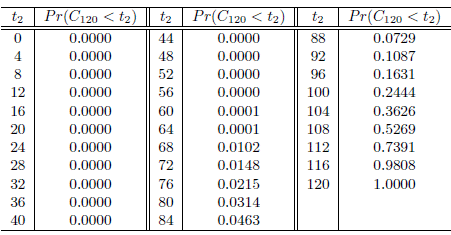
Los valores de la Cdf del tiempo operacional acumulativo, para la estructura reparable en serie, con dos unidades, son mostrados en el Tabla 2 y Figura 2.
Con las especificaciones que se dieron para la estructura en serie con dos unidades, se puede deducir lo siguiente: las probabilidades bajas indican como poco probable que el tiempo acumulado de la estructura funcione menos de t 2 horas; la probabilidad de que el tiempo acumulado de funcionamiento del proceso sea menor a 92 horas, es de 0.1087; la probabilidad de que el tiempo acumulado de funcionamiento del proceso sea menor a 108 horas, es de 0.5269.
En el Tabla 3 se presenta tres ejemplos. En cada uno de ellos se asume dos unidades A y B que se encuentran en perfectas condiciones. Los tiempos esperados de vida, reparación y mantenimiento se conservan fijos. Varía el tiempo de funcionamiento de cada unidad antes de entrar a mantenimiento preventivo y el tiempo de misión.
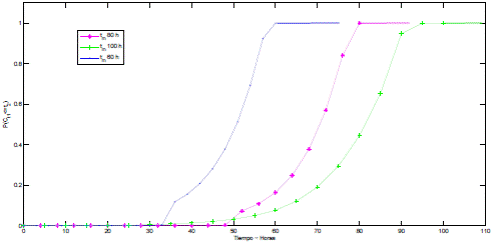
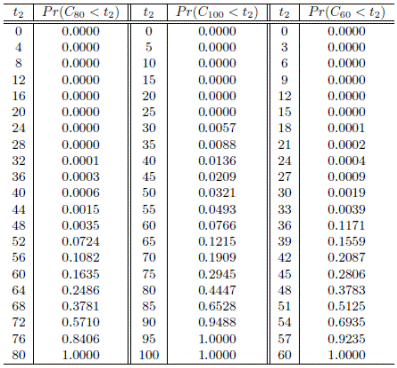
Los valores de la función de distribución acumulativa (Cdf) del tiempo operacional acumulativo para un tiempo de misión de 80, 100 y 60 horas son presentados en la Figura 3 y en la Tabla 4.
De los tres tiempos de misión se puede deducir lo siguiente: para un t m = 100 h se observa que, con una probabilidad de 1, el tiempo acumulado de funcionamiento del proceso se termina en menos de 95 horas; para un t m = 80 h la probabililidad de que el tiempo acumulado de funcionamiento del proceso sea menor a 76 horas, es de 0.8406, y para un t m = 60 h, la probabililidad de que el tiempo acumulado de funcionamiento del proceso sea menor a 57 horas, es de 0.9235.
En un t m = 60 h se observa que entre los tiempos t 2 = 33 y t 2 = 36 horas, la estructura puede presentar alguna alteración; dicha anomalía se puede ver por el valor de las probabilidades: de 0.0039 pasa a 0.1171; para el t m = 100 h, la estructura puede presentar anomalía. Entre los tiempos t 2 = 65 y t 2 = 70 horas se observa que, de 0.1215, pasa a 0.1909, y para un t m = 80 h, la estructura puede presentar anomalía. Entre los tiempos t 2 = 56 y t 2 = 60 horas se observa que, de 0.1082, pasa a 0.1635.
6 Conclusiones
Los procesos de renovación en la industria han sido motivo de muchas investigaciones. Una de sus temáticas es el estudio de la estimación de las características del tiempo operativo del sistema; por ejemplo, la función de distribución (cdf) del tiempo operacional acumulativo, en un intervalo finito
 , es representada en términos de disponibilidad de trabajo. La función de disponibilidad se modeló a través de un sistema de ecuaciones integrales de una estructura en serie reparable, con dos unidades, y la solución se encontró por medio de un método numérico, fijando el tiempo t
1 y variando el tiempo t
2.
, es representada en términos de disponibilidad de trabajo. La función de disponibilidad se modeló a través de un sistema de ecuaciones integrales de una estructura en serie reparable, con dos unidades, y la solución se encontró por medio de un método numérico, fijando el tiempo t
1 y variando el tiempo t
2.
En la función de distribución acumulativa (Cdf) del tiempo operacional acumulativo para un tiempo de misión t 1 se encuentra: probabilidades bajas, indican poca probabilidad de que el tiempo acumulado de la estructura funcione menos de t 2 horas; saltos de probabilidades, es decir, se observa cambios bruscos en el valor de probabilidades (se puede presentar alguna anomalía entre dos tiempos en el proceso). También, muestra el tiempo en que el proceso puede terminar su misión (cumple su objetivo); se resalta que se puede identificar si el tiempo acumulado de funcionamiento del proceso puede terminar en menos de t 2 horas, con gran probabilidad.