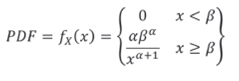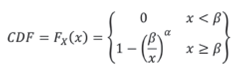Introduction
A radar is a device that radiates electromagnetic waves and gathers the echo produced by them on nearby objects (Richards, Scheer, & Holm, 2010). The mission of the radar is to detect targets of interest and to discard those that do not concern a particular application. Some objects (like clouds) can be considered as targets for certain applications (meteorology) and as interfering signal for others (aerial exploration).
When operating in coastal or offshore environments, the echo received from the sea surface is interpreted as an interference and called sea clutter (Ward, Tough, & Watts, 2013). The clutter is a random signal whose contribution cannot be deduced by purely deterministic mechanisms. Consequently, its modeling is accomplished through statistical distributions.
Several probability distributions with heavy tails have been used to fit sea clutter data. The Weibull (Ping, 2011), Log-Normal (Ishii, Sayama, & Mizutani, 2011), K (Chen, Liu, Wu, & Wang, 2013), KK (Watts & Rosenberg, 2013) and WW (Dong, 2006) distributions are among the most popular choices. Developments based on these distributions have been presented by the Radars Research Team from the Havana Technological University (González Padilla, Bravo Quintana, Machado Fernández, & Bueno González, 2013; Machado Fernández, 2015; Machado Fernández & Bacallao Vidal, 2016a; Machado Fernández & Bacallao Vidal, 2016b; Machado Fernández & Bacallao Vidal, 2016b; Machado Fernández, Bacallao Vidal, & Chávez Ferry, 2015).
Nevertheless, after reviewing the literature, the authors noted that the Pareto distribution has been gradually gaining acceptance in the modeling of sea clutter (Chakravarthi & Ozturk, 1991; Farshchian & Posner, 2010; Gelb, Heath, & Tipple, 2010; Piotrkowski, 2008; Watts & Rosenberg, 2013; G. V. Weinberg, 2013a). Actually, it has been suggested that this distribution provides better fits that the ones exhibited by the most popular alternatives (Farshchian & Posner, 2010). As a result, numerous recent investigations have applied the Pareto distribution in radar related applications (Mezache, Chalabi, Soltani, & Sahed, 2016; Rosenberg & Bocquet, 2015; Wang & Xu, 2014; Graham Victor Weinberg, 2013). The CUJAE's Radar Research Team has a great interest in developing Pareto based solutions, because this new model has a simpler PDF (Probability Density Function) compared to its counterparts K and KK, which will simplify the design and implementation of radar detectors.
Regardless of the distribution assumed as hypothesis, radar detectors always seek to ensure the CFAR (Constant False Alarm Rate) property and are designed, therefore, according to the Neyman-Pearson criterion (Barkat, 2005). The most commonly used are the CA-CFAR (Cell Averaging), the GO-CFAR (Greatest-Of), the OS-CFAR (Smallest-Of) and OS-CFAR (Ordered Statistics). These detectors have been addressed in the literature by several authors (Farina & Studer, 1986; Rohling, 1983; G.V. Weinberg, 2004) and are often used as reference in current projects (Caso & De Nardis, 2013; de Figueiredo, Bianco, Lenzi, & Figueredo, 2013; Qin & Gong, 2013; Takahashi, 2010).
In addition, each year new alternatives appear in different international journals. Some seek to introduce new processing methods (Qin & Gong, 2013; Van Cao, 2012), while others concentrate on improving existing ones (Magaz, Be-louchrani, & Hamadouche, 2011; Yadav & Kant, 2013).
Most implementations propose the use of different mechanisms for estimating the clutter average, which improves the response of the system against sudden changes in the background signal. However, the effect of the clutter statistical slow variation on the performance of the detector is often ignored.
Slow statistical changes are mathematically translated as a fluctuation of the shape parameter of the clutter distribution assumed as hypothesis. Several publications have verified that the shape parameter may vary in a wide range of values for different environmental conditions and radar features (Chen et al., 2013; Dong, 2006; Greco, Bordoni, & Gini, 2004; Ishii et al., 2011; Nohara & Haykin, 1991; Palama, Maria, Stinco, & Gini, 2013).
Moreover, in (Machado Fernández & Bacallao Vidal, 2014) it was verified that the fluctuation of the shape parameter causes significant problems in the performance of the CA-CFAR scheme. If the threshold multiplier factor (7), included in most implementations, is not modified according to the shape parameter variation, the detector will lose the CFAR property, experiencing serious deviations from the design false alarm probability (Machado Fernández & Bacallao Vidal, 2014). Unfortunately, the classical CA-CFAR detector is intended to operate with a fixed factor, which makes the system unstable.
Taking into account the previously presented ideas, the authors aimed to obtain estimates of the optimal threshold multiplier factor (T) for each possible value of the Pareto shape parameter, for a CA-CFAR detector with 64 cells in the reference window. The estimation was carried out for the false alarm probabilities of Pf = 102, Pf = 103 and P{= 104. Therefore, the objective was to create an adaptive CA-CFAR that will use the found values for constantly correcting the threshold multiplier.
It was assumed as hypothesis that the clutter was Pareto distributed with known shape parameters. The CA-CFAR scheme was used as the base of the design because it is the more widely used alternative.
The main contribution of the paper is the finding of mathematical expressions that allow the estimation of for any Pa-reto shape parameter in the range of possible values. It was verified through simulations, that the offered expressions ensure keeping the false alarm probability with a reduced deviation from the design value when processing clutter with slow statistical variations.
The paper proceeds as follows. The next section, under the name of "Materials and Methods" makes a brief presentation of the Pareto distribution and the CA-CFAR detector, describing also the performed experiments. Then, in "Results and Discussion", the authors reveal the relationship found between the CA-CFAR and the Pareto shape parameter. Afterwards, mathematical expressions are derived as a generalization of the performed simulations. Finally, in "Conclusions and Future Research", the fundamental contributions of the paper are summarized and the future research lines are discussed.
1. Materials and methods
This section starts by introducing the fundamentals of the Pareto distribution. In a second sub-section, the CA-CFAR detector is briefly described. Finally, the details of the executed experiments are presented to facilitate the replication of the research by third parties.
Pareto Distribution
The Pareto distribution has been used in modeling the income of a population (Asimit, Furman, & R. Vernic, 2010) and in a variety of engineering fields (Aban, Meerschaert, & Panorska, 2006; Chlebus & Ohri, 2005; Rytgaard, 1990), also including sonar (Gelb et al., 2010) and radar (Chakravar-thi & Ozturk, 1991; Farshchian & Posner, 2010; Piotrkowski, 2008) applications. Particularly in (Farshchian & Posner, 2010), the distribution was examined for the representation of high-resolution X-band sea clutter observed at low razing angles. This investigation showed that the distribution provides an accurate fit to polarized clutter returns, outperforming other classical models such as the Log-Normal, Weibull, K, KK and WW
It was also reported that the closest competitor to Pareto was the KK model. As the Pareto distribution is characterized by a simple PDF, the results are promising. It's suggested that the Pareto distribution will become a natural replacement of the KK which uses between 4 and 5 parameters with a complicated PDF including Bessel functions.
The PDF and the CDF (Cumulative Distribution Function) of the Pareto distribution are given below:
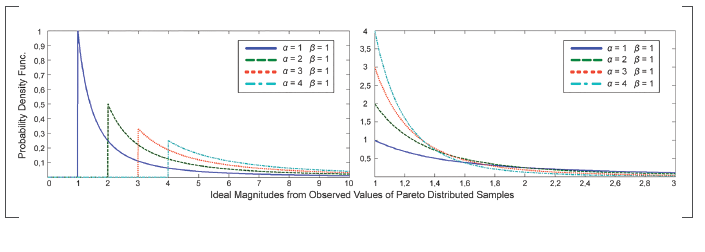
Where α is the shape parameter and β is the scale parameter (G. V. Weinberg, 2011), also referred to as location parameter or x - minimun value (O'Connor, 2011). The β parameter specifies the region where the distribution exists, which always covers the interval [β,∞] . Meanwhile, the shape parameter controls how fast the tail of the distribution falls. Figure 1 shows the effect of the variation of the parameters on the Pareto PDF.
Multiple fits made in Graham V. Weinberg, (2014) resulted in the following combinations of the Pareto parameters: (α = 15,9; β = 0,1812), (11,393; 0,3440), (4,4525; 0,0147) and (4,7245; 0,0446). In addition, simulations performed in Metcalf, Blunt, & Himed, (2015) applied the following reference interval for the shape parameter: 3,2< α 40; whereas in G. V. Weinberg, (2013b) the next values were used: 2,29 < α < 56,5215.
Taking into consideration the above information, the authors decided to use the following range of values to execute the experiments: 2 < α < 10. The α > 10 interval was excluded after noticing that the selection of T remained virtually constant in this region.
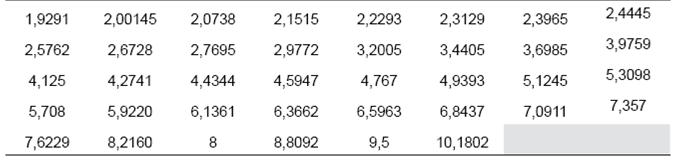
Initially, ten equally spaced values were used within the selected range to perform the experiments. As a response to the observed behavior, it was decided to add more a values in the regions that proved to have a greater influence in the selection of the T factor. The 38 T values that were finally used in the simulations are included in Table 1, ordered from left to right and from top to bottom.
CA-CFAR Processor
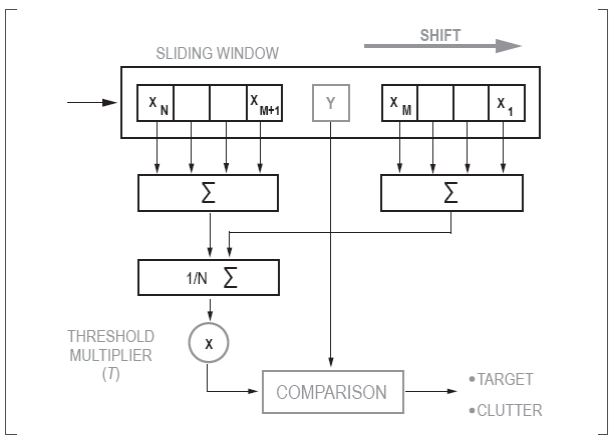
The internal structure of the classical CA-CFAR processor is shown in Figure 2 (Rohling, 1983). It consists of a sliding window that moves throughout the radar coverage area, giving each resolution cell an opportunity to occupy the slot under evaluation (Y ). The detection threshold is calculated by averaging the Xn cells and multiplying the result by T. The detector indicates the presence of a target in the slot under evaluation if the magnitude of Y exceeds the calculated threshold (Machado Fernández & Sánchez Rams, 2016).
The selection of the T value to be used is influenced by the clutter statistics, the false alarm probability and the number of cells (n) in the reference window. Usually, the detector operates with a preset window size and a fixed false alarm probability. In its original configuration, the CA-CFAR establishes a constant T value because it assumes that the clutter statistical behavior is invariable. In practice, when statistical variations occurs, meaning the clutter shape parameter is fluctuating, the operational false alarm probability deviates from the intended design value (Machado Fernández & Bacallao Vidal, 2014).
Conducted simulations
The conducted simulations aimed at correcting the above problem. First, the Set A was assembled, consisting of 38 groups of 1 million Pareto samples each. The Pareto samples were computer-generated by using one of the α values presented in Table I for each group.
Then, the first group of samples was processed with a CA-CFAR whose reference window had 64 cells. A random T value was used in the first iteration and the obtained Pf was recorded. Next, the Tvalue was modified in successive iterations forcing the Pf to reach the figures of 102, 103 and 10-4, with an error of less than a 1%.
Given the inverse relationship between the T and the Pf (Machado Fernández, 2015), the implemented algorithm was actually a binary search where T was increased whenever a reduction of the Pf was necessary, and vice versa. The sequence of steps was repeated for each group, requiring about 25 iterations to produce each T value with I the specified accuracy.
The β parameter of the Pareto distribution was forced to 0,001 for all simulations. This parameter defines the minimum possible value of the received samples, which is very small for radar applications. The β parameter was conceived for the initial applications of the distribution when it was used for modeling the income of a group of people. The β parameter allowed establishing the minimum salary. On the contrary, as it was demonstrated in Machado Fernández & Bacallao Vidal, (2014), the scale parameter of the statistical distributions has no influence of the detection performed by a CA-CFAR scheme.
2. Results and Discussion
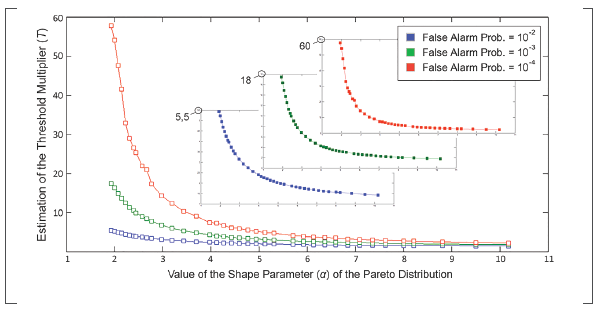
As a result of the conducted experiments, three T values were produced from each group of samples. This makes a total of 114 T values, where 38 correspond to Pf=102, and an equal number to Pf =10-3 and Pf =10-4. The obtained results are summarized in Figure 3 that reveals the influence of α on the modification of Tfor the three addressed Pf . In addition, three graphs placed within Figure 3, plot individually the data for Pf = 102, Pf =103 and Pf=104, proving that the tendency is common for all three cases.
Source: The author
Figure 3 Optimal values for multiple statistical conditions of Pareto distributed clutter
As it can be seen, α small modification in the region of reduced a values requires a significant correction of T in order to maintain the design Pf . However, for α > 7, the behavior is close to linear, with a marked tendency of T to remain constant. So, it's safe to say that the influence of α over T gets saturated.
The CA-CFAR threshold multiplier is an excellent measure of the spiky property of a distribution. The Pareto clutter is more spiky as the a value gets smaller, characteristic it shares with the K distribution according to that observed in Machado Fernández, (2015); Machado Fernández & Bacallao Vidal, (2016b). On the contrary, the Log-Normal distribution histograms have longer tails for high values of the shape parameter (Machado Fernández & Bacallao Vidal, 2016a).
Deviation of the false alarm probability
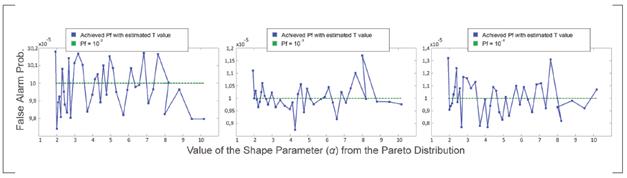
Next, the authors created a new set (Set B) with the same dimension of Set A but completely independent from it. The T values found with the Set A were used to process the samples from Set B in order to find the deviation experienced in the false alarm probability. The results are plotted in Figure 4 for Pf =102, Pf =103 and Pf=104.
As the reader may notice, both positives and negatives errors occurred, representing a desired behavior. The exact figures for the average deviation were: 1,1247 10-4 for Pf = 10-2; 3,5500 10-5 for Pf =103; and 1,1184105 for Pf=104. Therefore, it was demonstrated that the Testimated values ensure the operational false alarm probability will remain close to the design value regardless of the used dataset.
Fitting the results
The T values shown in Figure 3 can be applied when the Pareto clutter corresponds to any of the shape parameters included in Table 1. However, it's necessary to generalize the results for the entire region of possible occurrences of the parameter (2 < α < 10). Thus, a Testimate will be available for any statistical condition of the Pareto clutter.
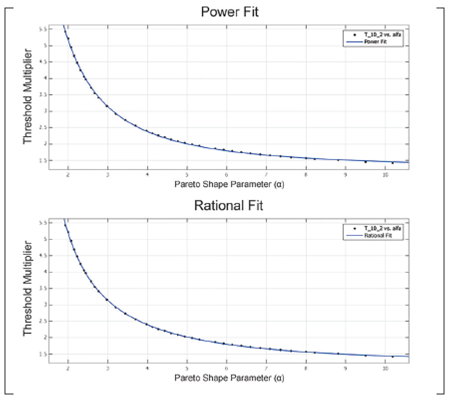
To this end, the authors tested different curve fittings searching for a good approximation to the observed behavior. The best match was exhibited for the power and rational fits. The expressions found through the fits are offered in Tables 2 and 3, together with the measured RMSE (Root Mean Squared Error).
Moreover, Figure 5 shows the accuracy achieved by the two fits. Both alternatives showed a good proximity to the data. Nevertheless, the numerical comparisons indicated that the power fit was slightly more accurate for Pf= 10 2, and slightly worst for the other two false alarm probabilities.
Source: The author
Figure 4 Experienced deviation in the operational false alarm probability after processing Set B.
The T values corresponding to the as from Table 1 were re-calculated using the obtained fits. The result was compared to the ones obtained with the T values from Figure 3. Figure 6 plots the error introduced by the power and rational approximations. As it can be observed, the greatest errors occurred in the region of small magnitudes of α,a fact that can be explained given the great influence of the shape parameter over T selection in this region. However, the overall mistake is small, confirming therefore the quality of the fit.
The error for Pf= 102 was 0,0147 for the power fit and 0,0094 for the rational fit. The quantities were 0,1108 and 0,0762 for Pf= 10-3 and 0,7750 and 0,6451 for Pf= 10 4. So, only a very small error is introduced when replacing the binary search estimates for the mathematical expressions, being more accurate the rational fit.
Validation of the fit
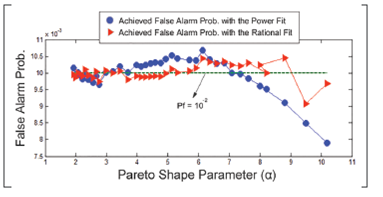
Besides checking the existing proximity between the T values extracted from the experiments and those calculated by expressions from Tables 2 and 3, the authors conducted a further test to ensure validation. The T values obtained through the fits were used to process data from Set B with a 64 cells CA-CFAR. The experienced deviation in the false alarm probability is plotted in Figure 7 for Pf = 10-2.

Source: The author
Figure 6 Deviation in Tvalues after using the Power and Rational fits for the false alarm probabilities of 1 0 2, 10 3 y 1 0-4
Source: The author
Figure 7 False alarm probability achieved by using the threshold multipliers calculated from the power and rational fits.
As the figure shows, the deviation suffered by the rational fit is smaller than the one experienced by the power fit for Pf = 10-2. A similar behavior was observed for the other two addressed false alarm probabilities.
The mean deviation for P- = 102 was 3,3866 104 for the power fit and 1,6708-10-4 for the rational fit. The numbers were 1,3445-10-4 and 8,7868-10-5 for P- = 10-3; and 3,6421-10-5 and 2,9789-10-5 for P- =10-4.
As expected, the error increases with the reduction of the false alarm probability due to the fixed amount of samples included in each of the groups from both sets (one million samples). Note that P- = 102 means 10.000 errors were committed for a million samples; whereas Pf = 10-4 represents the occurrence of only 100. So an important conclusion can be extracted from the study: in order to obtain a deviation close to 1% the trials must include at least 10.000 errors.
About the application of the results
Undoubtedly, the main contribution of the paper is the finding of mathematical expressions for estimating the optimal CA-CFAR threshold multiplier factor for any occurrence of the Pareto shape parameter in the 2 < α <10 interval. The found Tvalues are acceptable when compared with others offered in similar studies (Machado Fernández, 2015; Machado Fernández & Bacallao Vidal, 2016a; Machado Fernández & Bacallao Vidal, 2016b) and they ensure that the CA-CFAR will operate with a reduced Pf deviation, whenever the shape parameter is known a priori, even if the clutter exhibits statistical variations.
At the same time, this research completes one of the two requirements needed to create a CA-CFAR detector that operates without knowledge of the shape parameter. The other requirement is the estimation of the shape parameter that can be done using the MLE (Maximum Likelihood Estimation) method as it was applied in Forbes, Evans, Hastings, & Peacok, (2011); G. V. Weinberg, (2011). This estimation is mandatory because it's the base of the proposed solution, which assumes the shape parameter is already known.
Additionally, a solution that uses artificial neural networks as an improved shape parameter estimator was successfully developed in Machado Fernández et al., (2015) for the Weibull distribution and in Machado Fernández & Bacallao Vidal, (2016a) for the K model. The similarity between this two distributions and the Pareto, suggests that the neuronal alternative could be also applicable to the Pareto case.
3. Conclusions and future research
Mathematical expressions for estimating the optimal value of the threshold multiplier factor were found for a 64 cells CA-CFAR scheme operating under the assumption of Pa-reto distributed clutter with a priori known parameters. The authors demonstrated that the offered expressions guarantee the detector will operate with a reduced deviation of the false alarm probability even if the Pareto shape parameter varies over a wide range. Therefore, the solution ensures the adaptation of the detector to slow clutter statistical changes that, despite being ignored by most of the previously presented solutions, have a proven influence in the detection performance. In addition, an important requirement was fulfill for the design of a processor capable of adapting to the clutter statistical changes without a priori knowledge of the shape parameter of the distribution.
This research contributes to the development of the theory of the Pareto distribution that has found recent application in sea clutter modeling. It was verified that the influence of the Pareto shape parameter is significant for the lower figures of the parameter and is rapidly saturated with its increase. Recommendations were also offered on the number of trials to be performed in order to obtain reliable estimates of the multiplicative factor for a given false alarm probability.
The authors will focus next on performing similar estimates for other clutter related distributions such as the Compound Gaussian and KK. The design of a neural solution for the improved estimation of the Pareto shape parameter is also recom-mended.