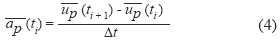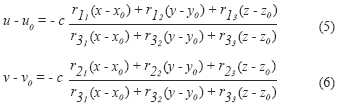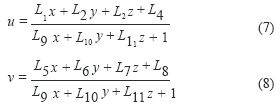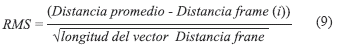Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
Revista Ingeniería Biomédica
versão impressa ISSN 1909-9762
Rev. ing. biomed. vol.3 no.6 Medellín jul./dez. 2009
DETECCIÓN, RASTREO Y RECONSTRUCCIÓN TRIDIMENSIONAL DE MARCADORES PASIVOS PARA ANÁLISIS DE MOVIMIENTO HUMANO. CINEMED II
Christian Andrés Diaz1,2, Maria Luisa Toro1, Johana Carolina Forero1, Andrés Torres1
1 Línea de biomecánica e Ingeniería de rehabilitación. Grupo de investigación en Ingeniería Biomédica EIA-CES (GIBEC), Colombia.
2 Dirección para correspondencia: bmchidia@eia.edu.co.
Recibido 23 de octubre de 2009. Aceptado 11 de diciembre de 2009
RESUMEN
Uno de los desafíos más importantes cuando se desarrolla un sistema de análisis de movimiento es la reconstrucción tridimensional, ya que este proceso involucra una serie de algoritmos que tienen que trabajar de forma sinérgica con el fin de reconstruir el movimiento correctamente y aminorando el número de intervenciones del usuario. Por esta razón en este artículo, se realiza una descripción detallada de un esquema para la reconstrucción tridimensional del movimiento humano mediante la integración de diferentes algoritmos que a su vez minimizan la intervención del usuario durante el proceso (Sistema de análisis de movimiento CineMED II). Para probar el desempeño del esquema propuesto se realizaron tres pruebas experimentales; un marcador estático, barra con dos marcadores en movimiento y dispositivo de medición de errores. Obteniendo finalmente que CineMED II posee un desempeño cercano al de los sistemas comerciales, mostrando en las pruebas realizadas con la barra un error absoluto medio menor respecto al sistema Vicon, pero mayor con respecto al sistema Elite y en las pruebas con el dispositivo un valor de RMS mayor respecto al sistema Ariel, pero un error máximo menor respecto a este ultimo sistema, sin embargo la aproximación propuesta presenta problemas cuando se ocluyen marcadores por largos periodos de tiempo y cuando se cruza la trayectoria de dos marcadores. Para resolver dichos problemas se propone adicionar algunas cámaras al sistema y así obtener información redundante de la captura del movimiento.
PALABRAS CLAVE: Análisis de movimiento, Digitalización de marcadores, Rastreo de marcadores, Reconstrucción tridimensional de marcadores.
ABSTRACT
One of the most important challenges when a movement analysis system is been developed is the three-dimensional reconstruction. This process involves several algorithms that must work synergistically in order to reconstruct the movement correctly and decreasing the user interventions. For this reason this paper describes in detail a new methodology to carry out the three-dimensional reconstruction of the human movement through the join of different algorithms decreasing the user input during the process (movement analysis system CineMED II). To analyze and evaluate the performance achieved using the methodology proposed, three experimental tests were carried out; a static marker test, bar with two markers in motion and using an error measurement device. CineMED III finally has a performance close to that of commercial systems, showing in the tests performed with the bar a lower average absolute error for the Vicon system, but higher with respect to the Elite system and testing the device with a value of RMS more about the Ariel system, but a smaller maximum error on the latter system., However, the proposed approach presents problems when markers are occluded for long periods of time and when the paths of two markers intersect. To solve these problems, it is proposed to add some cameras into the system to obtain redundant information from the motion capture.
KEY WORDS: Movement analysis, Markers digitization, Markers tracking, Markers tridimensional reconstruction.
I. INTRODUCCIÓN
En el área de estudio del análisis del movimiento humano, la técnica más utilizada en los diferentes campos de aplicación, ya sea clínico, biomecánico o deportivo ha sido el rastreo óptico [1]. Las técnicas de rastreo óptico hacen uso de múltiples sensores de imágenes bidimensionales (cámaras) para estimar la posición de una persona, herramienta u objeto. Usualmente para llevar a cabo el rastreo del movimiento de un cuerpo, estos métodos hacen uso de patrones o de marcas reflectivas [2-3] (estos serán llamados marcadores) ligadas a dicho cuerpo con el fin de facilitar mediante el contraste la identificación de los puntos anatómicos que requiere el sistema, para que posterior a la reconstrucción tridimensional se pueda calcular el modelo biomecánico del movimiento desarrollado. A partir de las imágenes tomadas por los sensores se aplican en general tres módulos con el propósito de realizar la reconstrucción tridimensional del movimiento: el módulo de digitalización de los marcadores el cual se encarga de definir la ubicación en la imagen de los marcadores; el módulo de correspondencia, el cual como su nombre lo dice determina la correspondencia en cada una de las cámaras de los marcadores y finalmente el módulo de reconstrucción tridimensional que usa las coordenadas bidimensionales resultantes de la detección y la información de correspondencia para hallar las coordenadas espaciales del marcador.
Actualmente existen diferentes tipos de sistemas de análisis de movimiento como por ejemplo los que utilizan cámaras directamente conectadas al computador [4], dispositivos magnéticos y mecánicos [5], entre otros. Los que emplean video cámaras o de rastreo óptico, se caracterizan por utilizar mínimo cinco de estos dispositivos; ya que para que un marcador pueda ser reconstruido, tiene que ser visto al menos por dos cámaras y adicionalmente utilizan sus propios métodos para el análisis de los datos. En base a lo anterior se planteó construir un sistema de análisis de movimiento compuesto por cuatro cámaras, semi-automático, que logre minimizar el número de intervenciones del usuario (CineMED II).
Los sistemas de análisis de movimiento permiten la recolección de información para ilustrar y analizar la dinámica del movimiento, al estudiar las características de los miembros del cuerpo y las articulaciones [6]. Los resultados obtenidos de estos análisis, ofrecen al personal del área de la salud una herramienta de apoyo diagnostico, para contar con información que les permite realizar una evaluación objetiva por ejemplo de patologías ortopédicas, recomendar un tratamiento especifico, evaluar la evolución de una terapia, así como también aplicarlo en otros ámbitos como el análisis de diferentes gestos deportivos [1], entre otras múltiples aplicaciones.
Para poder lograr que estos resultados objetivos sean confiables, es necesario contar con un sistema robusto que sea capaz inicialmente de identificar los marcadores, determinar la correspondencia y reconstruir tridimensionalmente la posición del cuerpo que está siendo analizado, para que así se puedan hacer posteriores cálculos del sistema biomecánico con el fin de encontrar los diferentes parámetros que son objeto de estudio.
En este artículo, se realiza una descripción detallada de la integración de varios algoritmos para obtener la reconstrucción tridimensional del movimiento humano minimizando la intervención del usuario durante el proceso (CineMED II). Para probar el desempeño del sistema propuesto se realizaron tres pruebas experimentales; un marcador estático [7], barra con dos marcadores en movimiento [8] y dispositivo de medición de errores [7] así como también una prueba piloto con un paciente amputado para realizar la reconstrucción tridimensional del gesto de la marcha humana.
II. MATERIALES Y MÉTODOS
CineMED II está diseñado en la plataforma C#.NET 2005, para inicialmente capturar videos de cuatro cámaras de alta velocidad Fastec Imaging (250 frames por segundo) que graban el movimiento específico que posteriormente se analizará. Estas cámaras están ubicadas en los vértices de un cuadrado de 5x5 metros y a 2 metros de altura. Además, están sincronizadas usando el modo de las cámaras "trigger", estas son conectadas a un hardware externo conformado básicamente por un pulsador que cuando es activado envía la señal a las cámaras para iniciar la captura en el mismo instante de tiempo. El espacio físico donde se realizan las grabaciones para su posterior análisis, es un espacio con iluminación controlada para disminuir el ruido que ocasiona la luz ambiental. A continuación se describen los métodos utilizados para la implementación de los algoritmos de detección, rastreo y reconstrucción tridimensional de marcadores pasivos.
2.1 Módulo de digitalización:
El objetivo de este componente de los sistemas de rastreo óptico, es determinar las coordenadas planares en la imagen de cada uno de los marcadores. De la exactitud y precisión de este módulo del sistema, depende la calidad de las variables cinemáticas entregadas [9].
El algoritmo de digitalización de los marcadores en CineMED II se propuso automático, mediante el manejo de condiciones controladas de iluminación y está compuesto por tres componentes: detección de movimiento, extracción de características y definición de la trayectoria (Fig. 1).
- Algoritmo de detección de movimiento:
Este algoritmo se implementa para así ahorrar el procesamiento de la imagen completa en subsecuentes pasos. Consiste inicialmente en una segmentación que se logra, restando la imagen de fondo de la escena y la imagen del frame actual donde se desee determinar la ubicación del objeto en movimiento; posteriormente se realiza una división de la imagen resultante por pixeles para definir los bordes de la persona u objeto en movimiento en la escena; luego se binariza la imagen en el espacio de colores RGB (Red, Green, Blue) obteniendo así la zona donde se está realizando el movimiento de un color completamente blanco. Finalmente mediante otro algoritmo se determinan los límites superior, inferior, derecho e izquierdo de la zona blanca demarcada, m encionada anteriormente.
- Algoritmo de extracción de características:
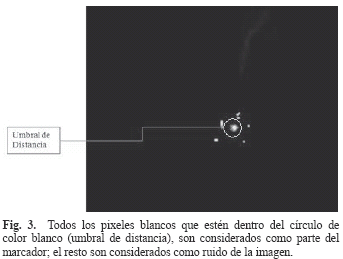
Este algoritmo determina en qué sitio de la imagen segmentada por el algoritmo anterior, hay un posible marcador. Para este fin, se implementó el método de binarización por luminancia, el cual permite detectar los marcadores a partir de sus propiedades de brillo y tamaño. Con el propósito de determinar los puntos brillantes que pueden haber en la imagen, ésta es transformada del espacio de colores RGB al HSL (Hue, Saturation, Lightness). Luego, utilizando como parámetro la luminancia se binariza la imagen, quedando las regiones donde se encuentra un posible marcador de color blanco y el resto de la imagen de color negro [10] (Fig. 2). Posteriormente, las coordenadas de los pixeles de color blanco en la imagen binaria son agrupadas usando como criterio un umbral de distancia, donde los pixeles que se encuentran dentro del umbral son considerados como parte del marcador y son sumados para determinar el tamaño de este; el resto son considerados como ruido de la imagen (Fig. 3). Adicionalmente con el fin de determinar si un grupo de pixeles blancos corresponde a un marcador o a cualquier elemento considerado como ruido, se establece un parámetro, el cual define el número mínimo de pixeles blancos que debe tener cada grupo de tal manera que pueda ser considerado un marcador.
2.2. Módulo de correspondencia:
- Módulo de rastreo:
Una vez se han detectado los marcadores para cada frame de cada cámara utilizada para el análisis de movimiento, se procede al rastreo de los marcadores para construir sus trayectorias, donde se selecciona el vínculo correcto para la misma partícula desde un instante de tiempo al siguiente [11]. Para esto, los primeros dos frames de cada cámara son intervenidos manualmente por el usuario, dando clic sobre cada marcador en la imagen en un orden determinado. A partir del tercer frame para cada una de las cámaras se utiliza el algoritmo de ventana móvil [1] para el rastreo, aplicando los siguientes criterios para una asignación efectiva de un marcador de un instante de tiempo al siguiente:
- La velocidad de las partículas es limitada en los tres componentes del vector de movimiento. Así, para una posición 3D
 de una partícula en un tiempo ti, y su posición en el instante de tiempo siguiente ti+1 se predice asumiendo que la partícula tiene una velocidad constante
de una partícula en un tiempo ti, y su posición en el instante de tiempo siguiente ti+1 se predice asumiendo que la partícula tiene una velocidad constante 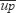
- Es posible utilizar una extrapolación lineal si la partícula tiene un vínculo en tiempo anterior ti-1, sino, la posición misma xp en ti se utiliza como posición de búsqueda [11].
- La aceleración Lagrangiana de la partícula (diferencia de dos vectores de velocidad consecutivos de una partícula) es limitada; lo que define un área de búsqueda cónica. En caso de ambigüedades la asignación con la aceleración Langragiana menor es la más probable [11]. La búsqueda es realizada asumiendo que la aceleración es constante
 , así: Donde,
, así: Donde,
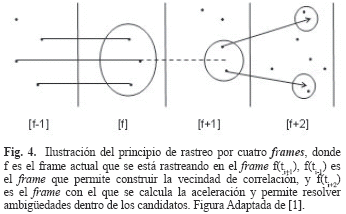
Con base en estos criterios se utiliza el método de la ventana móvil de cuatro frames [1], que supone que el desplazamiento del marcador del frame f(ti-1)[f-1] al frame f[f], predice la posición en f(ti+1)[f+1]. Luego utilizando esta posición y la proyección del movimiento a f(ti+2)[f+2] confirma la hipótesis con el fin de eliminar ambigüedades. Pueden existir tres casos para cada marcador en f[f] que se desea rastrear en f(ti+1)[f+1]: - El marcador tiene un vínculo en f(ti-1)[f-1]: en este caso se calcula el desplazamiento de f(ti-1)[f-1] a f[f], este se aplica a la posición en f[f] manteniendo la dirección del movimiento. Una vez se tenga la posición predicha, se define una vecindad de búsqueda en f(ti+1)[f+1] centrada ésta. Si en esta área se encuentra más de un marcador, se prolonga el movimiento a f(ti+2)[f+2] de la misma manera para cada candidato en f(ti+1)[f+1]. Por último, la trayectoria que tenga la menor aceleración entre f(ti-1)[f-1] y f(ti+2)[f+2], determinará el rastreo de f[f] a f(ti+1)[f+1] (Fig. 4).
- El marcador no tiene vínculo en f(ti-1)[f-1]: en este caso se define una vecindad de correlación en f[f], centrada en la posición actual del marcador en dicho frame. En esta región, deberán existir marcadores cuyo movimiento esté correlacionado con el marcador objetivo. Se utilizan los vínculos de f(ti-1)[f-1] a f[f] de estos marcadores para determinar el movimiento a aplicar en el marcador objetivo y se procede como en la opción anterior.
- Ninguna de las anteriores: se define como centro de la región de búsqueda, la posición en la que se encuentra actualmente el marcador.
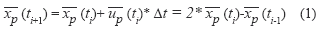 y
y 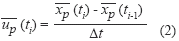
- Módulo de reproyección:
Con el fin de poder encontrar la correspondencia entre las cuatro imágenes (una por cada cámara) en cada instante de tiempo para el posterior proceso de reconstrucción tridimensional, se implementó un algoritmo que calcula la matriz fundamental. Esta matriz describe completamente la relación geométrica entre puntos correspondientes de un par de cámaras [12]; dicha matriz se calcula a partir de mínimo 8 puntos conocidos y correspondientes entre dos imágenes. De esta manera, cuando al conocer un punto P1 en la imagen 1 y se quiere conocer cuál es el punto P1 en la imagen 2, correspondiente a P1 en la imagen 1; se multiplica la matriz fundamental por el punto conocido y esto da como resultado los parámetros de la línea epipolar, sobre la cual se encontrará el punto correspondiente. La matriz fundamental se calcula durante el proceso de calibración, utilizando los dispositivos de calibración que serán descritos más adelante. Para este sistema se ha planteado utilizar dos métodos con el fin de determinar la correspondencia entre los marcadores; el primero de ellos utiliza información tomando grupos de tres cámaras y aplica conceptos de matriz fundamental, geometría epipolar y reproyección; el segundo utiliza información tomando grupos de dos cámaras y aplica solo conceptos de matriz fundamental y geometría epipolar. Cuando se tienen más de tres cámaras en la configuración del sistema, es posible llevar a cabo dos aproximaciones. La primera de ellas es realizar el análisis tomando grupos de tres cámaras o dos como se menciono anteriormente. La otra posibilidad es aplicar el algoritmo de geometría epipolar entre dos cámaras y posteriormente aplicar el algoritmo de reproyección sobre las cámaras restantes.
- Algoritmo de reproyección:
Es posible conocer la reproyección de un marcador si se sabe su coordenada tridimensional y los parámetros de la cámara en la cual se desea conocer la reproyección. El término reproyección se refiere a calcular la posición bidimensional de un marcador en una cámara determinada partiendo de la posición tridimensional en el espacio conocida y es útil cuando se usa un sistema de reconstrucción tridimensional con más de dos cámaras y se desea saber si un marcador que ya fue reconstruido usando un par de cámaras, está presente en las cámaras restantes. De esta manera, es posible conocer las coordenadas, en la imagen del marcador reconstruido.
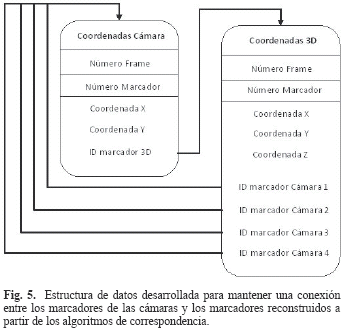
Para poder implementar los algoritmos descritos, es necesario crear una estructura de datos que conecte los marcadores reconstruidos (marcadores tridimensionales) con los marcadores detectados en las imágenes de cada una de las cámaras, esto con el objetivo de controlar los marcadores en las imágenes que son utilizados para el proceso de reconstrucción y de esta manera no incurrir en el uso de un mismo marcador dos veces o dejar de usar alguno. Para mantener una conexión entre estos dos arreglos se le asignó un ID (identificación) a cada uno de los marcadores de las imágenes de las cámaras y a los marcadores que son reconstruidos. En la Fig. 5 se pueden observar las dimensiones que componen los arreglos utilizados en la estructura de datos, al igual que la relación entre las identificaciones y los arreglos.
Se puede observar que cada marcador de cada cámara tiene un ID asignado y este ID está relacionado con el marcador reconstruido, con el fin de saber cuáles marcadores correspondientes a una determinada cámara fueron utilizados para reconstruir dicho marcador. De igual manera a cada marcador en la imagen de la cámara se le asigna el ID del marcador reconstruido, con el fin de saber cual marcador de la cámara para la reconstrucción 3D fue utilizado.
- Algoritmo correspondencia de marcadores entre dos cámaras:
Usando los conceptos de matriz fundamental y geometría epipolar, es posible desarrollar un algoritmo que lleve a cabo un proceso de correspondencia de marcadores entre dos cámaras. Por ejemplo, si se desea realizar una correspondencia de marcadores entre la cámara 1 y cámara 2, usando la coordenada de un marcador detectado en la cámara 1 y aplicando la matriz fundamental que relaciona ambas cámaras, es posible determinar la línea epipolar de la cámara 2 sobre la cual debería estar el marcador detectado en la cámara 1. Sobre los marcadores detectados en la cámara 2 se determina el que esté más cerca de la línea epipolar, así pues, se puede decir que este marcador es el correspondiente al marcador tomado inicialmente de la cámara número 1. En la Fig. 6 se esquematiza este proceso, donde en la cámara 1 se observa la imagen de la vara con los dos marcadores, en la cámara 2 se observan las líneas epipolares pasando a través de los marcadores proyectados en esta cámara. El algoritmo busca los marcadores más cercanos a la línea epipolar correspondiente en la cámara dos y asigna el par de marcadores respectivo.
- Algoritmo correspondencia de marcadores entre tres cámaras
En el algoritmo pasado se usaron los conceptos de geometría epipolar y matriz fundamental, sin embargo, durante este proceso de correspondencia se podrían presentar errores producto del cálculo de la matriz fundamental, conllevando a realizar correspondencias erróneas. Si además se utiliza la información entregada por el cálculo de la reproyección, se podría realizar un proceso de correspondencia entre tres cámaras. Este algoritmo inicia realizando un análisis de correspondencia entre dos cámaras aplicando los conceptos de geometría epipolar y matriz fundamental, si esta correspondencia es cumplida, reconstruye el punto a partir de estas dos cámaras y aplica el algoritmo de reproyección para predecir la posición de ese mismo marcador en una tercera cámara, si hay un marcador dentro del umbral predefinido cercado a la predicción entonces, se hace una reconstrucción tridimensional usando las tres posiciones y se asignan los índices. Como se puede deducir este algoritmo es mucho más confiable que el anterior ya que utiliza más información (marcadores de tres cámaras) con el fin de determinar una correspondencia entre marcadores. En la Fig. 7 se ilustra este proceso, donde la correspondencia entre la cámara 1 y 2 es realizada usando las propiedades de geometría y línea epipolar. La correspondencia entre las cámaras 2 y 3 es realizada usando el algoritmo de reproyección descrito anteriormente.
- Solución de ambigüedades en el rastreo:
Existe la posibilidad que un marcador que ha sido detectado no pueda ser rastreado. Esto puede ser porque un marcador estaba ocluido y se vuelve visible de nuevo en el frame que se está analizando, o por cercanía entre dos marcadores y son detectados como uno solo, o porque se cruzan dos trayectorias [13]. Para solucionar estas ambigüedades, se utiliza un algoritmo que emplea la matriz fundamental y la reconstrucción tridimensional que será descrita posteriormente. En caso tal que no se pueda asignar el marcador faltante a ninguna trayectoria, se solicita la intervención del usuario.
2.3. Módulo de reconstrucción tridimensional:
Para la reconstrucción tridimensional de los marcadores por medio de las cámaras se implementó el método DLT (Direct Linear Transformation). Este consiste en la linealización de las ecuaciones que modelan el proceso de generación de la imagen en una cámara. Básicamente, la transformación de las coordenadas desde el plano 2D al espacio tridimensional es una proyección perspectiva que esta descrita por las siguientes ecuaciones de colinealidad [9,14]:
Donde x, y e z Z son las coordenadas en el espacio 3D del punto; X xo, yo e zo son las coordenadas 3D del centro de perspectiva; u y v son las coordenadas de la proyección en el plano de la imagen del punto; uo y vo es el punto de intersección entre el eje óptico y el plano de la imagen; c es la distancia focal y rij son los nueve cosenos directores que caracterizan la orientación de la cámara. Por medio de tratamientos matemáticos la ecuación anterior puede ser expresada de la siguiente manera [15]:
Donde L1 a L11 son los parámetros DLT. Las ecuaciones presentadas en (7) y (8) poseen catorce incógnitas, de las cuales 11 son parámetros DLT y 3 son las coordenadas del punto en el espacio. Debido a que las únicas variables conocidas son las coordenadas del punto proyectado en el plano de la imagen, para poder realizar la reconstrucción tridimensional del punto a partir de varias vistas de éste, es necesario determinar el valor de los parámetros DLT para cada una de las cámaras. Para este propósito se lleva a cabo un proceso llamado calibración [16], donde se hace uso de 27 puntos de control dispersos en el volumen de trabajo sobre 3 dispositivos de calibración (Fig. 8). La barra superior del dispositivo se encuentra a 1,10 m del nivel del suelo.
Para que el sistema sea soluble, mínimo dos cámaras deben ver el punto que será reconstruido tridimensionalmente. Sin embargo entre más cámaras se utilicen en la reconstrucción tridimensional más preciso será el proceso [17]. Para la solución del sistema se implementó el método de mínimos cuadrados [18].
2.4. Pruebas de funcionalidad:
Se realizaron tres pruebas con el fin de avaluar la funcionalidad y el error presente en CineMED II, teniendo las cámaras configuradas a 125 Hertz. Con las dos primeras se buscó determinar la precisión y exactitud numérica del sistema, mientras que con la tercera se buscó encontrar la confiabilidad para reconstruir todos los marcadores en cada frame.
- Prueba marcador estático:
Con base en la medición del error del marcador estático del dispositivo propuesto por [7], se realizó una prueba con un único marcador ubicado en medio del área de prueba durante 100 frames. Luego se evaluó el error cuadrático medio RMS, de la distancia entre la posición promedio y la posición en cada frame. Además, se analizó el error absoluto máximo asociado con la medida de la posición del marcador, definido por el valor mayor de la distancia descrita anteriormente.
- Prueba barra:
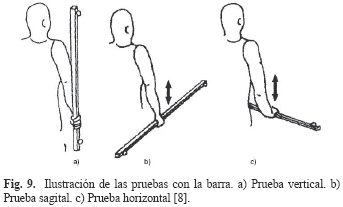
Se realizó una prueba con una barra de madera de color negro mate de 1 metro de largo, con dos marcadores pasivos ubicados en sus extremos a una distancia de 96 cm y cargada por un sujeto que marchaba en el área. La distancia entre estos fue calculada con base en los resultados de posición tridimensional en cada frame arrojados por el sistema [8]. Utilizando esta barra se realizaron tres pruebas. La primera con el antebrazo paralelo al torso y el extremo más alto de la barra aproximadamente a la altura de la mitad del tronco del sujeto que camina (Prueba vertical). En la segunda el sujeto marcha con la barra paralela al plano sagital (Prueba sagital) y en la tercera con la barra paralela al plano horizontal (Prueba horizontal). Estas dos últimas se realizaron moviendo la barra en dirección vertical. Cada uno de los videos de estas pruebas consta aproximadamente 300 frames. En la Figura 9 se ilustran las posiciones en las que está la barra durante las tres pruebas.
Los datos tridimensionales arrojados por el sistema se procesaron en hoja de cálculo para calcular la distancia y se evaluó además la media del error absoluto, equivalente al máximo valor de la media de los errores absolutos de la distancia entre los marcadores en cada una de las pruebas. También se calculó el error positivo máximo equivalente al máximo valor de la distancia entre dos marcadores menos el valor real para todas las muestras. Por último, el error negativo máximo equivalente al mínimo valor de la distancia entre dos marcadores menos el valor real de todas las muestras.
Esta prueba se realizó con el fin de simular el movimiento de marcadores pasivos en dirección de la proyección de la marcha.
- Prueba dispositivo:
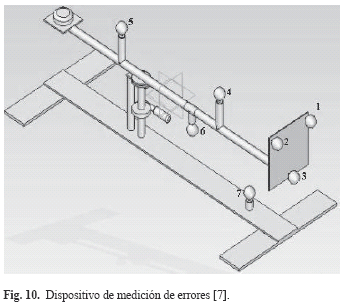
Esta prueba utilizó el dispositivo y la metodología descrita por [7], el cual soporta siete marcadores pasivos como se muestra en la Fig. 10. La posición del marcador ubicado por debajo de la barra fue variada entre 0, 1, 2 y 3 cm de distancia del marcador en la base de la barra, para un total de 4 pruebas.
Se calculó el promedio de la distancia entregada por el sistema de los dos marcadores de la parte superior del tubo horizontal, con la medida real 50cm y esto entrega el error absoluto promedio. Adicionalmente, se calcularon los errores absolutos para la medida de la distancia en cada frame y el mayor valor de estos se tomó como el máximo error absoluto. El ruido asociado a estas medidas para cada prueba fue calculado promedio del error cuadrático medio RMS que se calcula como la diferencia entre la distancia promedio y la distancia en cada frame (9).
Este procedimiento se siguió para los marcadores ubicados en la parte superior de la placa vertical, cuya distancia real es de 20 cm. Además, para el ángulo formado por los tres marcadores de la placa y con vértice en el marcador inferior. La medida de este ángulo es de 53,13 grados.
Por último, para el marcador estático ubicado en la base del dispositivo se calculó el RMS (9) entre el promedio de la posición tridimensional y la posición para cada frame (10).
Estos cálculos se realizaron para cada una de las pruebas.
- Prueba marcha:
Se realizó una prueba de marcha un sujeto de género masculino, usuario de una prótesis transtibial derecha, utilizando el modelo de Helen Hayes que utiliza 15 marcadores pasivos que se ubican en determinados puntos anatómicos, descrito por [19-20] e ilustrado en Fig. 11. Se trabajo con este tipo de paciente dado que el proyecto que enmarca la construcción de CineMED II está dirigido hacia esta población. Se configuraron las cámaras a una frecuencia de muestreo de 125 Hz. El gesto de la marcha incluye el balanceo de los brazos, el cual ocluye los marcadores ubicados sobre las crestas ilíacas anterosuperiores durante algunos instantes de tiempo para algunas cámaras.
III. RESULTADOS Y DISCUSIÓN
una vez realizadas las pruebas se realizo la comparación de los resultados con respecto a otros sistemas de análisis de movimiento que emplean cuatro cámaras (Vicon, Elite, Ariel, Qualisys) [7-8].
3.1 Prueba marcador estático:
En la tabla 1 se observan los resultados obtenidos para esta prueba calculando el error absoluto con respecto a todos los frames que componen el video.
3.2 Prueba barra:
En la tabla 2 se observan los resultados obtenidos en la medición del error absoluto del sistema, el error máximo positivo y el error máximo negativo, de acuerdo con lo planteado por [8].
El error absoluto máximo de la media tiene similar comportamiento para la prueba con la barra sagital y horizontal, y a la vez menos que con la barra horizontal. Esto se debe a que en la prueba con la barra horizontal, ambos marcadores eran vistos mínimo por tres cámaras, lo que contribuyo a la precisión de la medida. Mientras que para las pruebas sagital y vertical, ambos marcadores eran vistos en la mayoría de los casos únicamente por dos cámaras, eso disminuyó la precisión del sistema en estos casos, aunque no incremento considerablemente el error respecto a la prueba horizontal.
El error máximo positivo corresponde al frame 24 de la prueba sagital, instante donde cada uno de los marcadores fue visto únicamente por dos cámaras. El error máximo negativo corresponde al frame 13 donde al igual que en la descripción anterior, ambos marcadores eran vistos por dos cámaras.
En la tabla 3 se observa la comparación de estos resultados con los obtenidos por sistemas de análisis de movimiento que utilizan cuatro cámaras [8]. El error absoluto medio para el sistema propuesto, es similar al encontrado en los sistemas comerciales. El sistema Elite tiene un error absoluto medio menor que CineMED II, pero el sistema CineMED II tiene una mejor precisión comparado con el sistema Vicon. Con respecto a los errores máximos, el sistema CineMED II posee un error máximo menor que los dos sistemas comerciales con los que se comparo. Vale la pena anotar que en una de las metodologías de referencia [8] se garantizó que no hubiera oclusión de los marcadores en ninguna cámara durante toda la prueba realizada.
3.3 Prueba dispositivo:
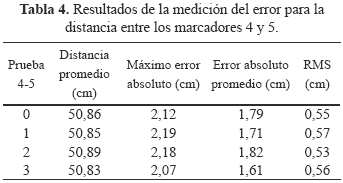
En la Tabla 4 se pueden observar los resultados de la medición del error para la distancia entre los marcadores 4 y 5 (Fig. 10). Los números de las pruebas representan la distancia horizontal entre el marcador 6 y 7 en cm.
Estos valores de RMS son mayores que el mayor presentado por [4] de 0,49 perteneciente al sistema Ariel. De la misma manera, este sistema fue el que presentó el máximo error de 1,66 cm, menor que el obtenido por el sistema Ariel.
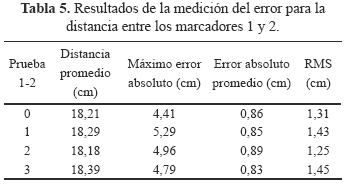
En la Tabla 5 se encuentran los resultados de la medición del error para la distancia entre los marcadores 1 y 2 (Fig. 10).
Durante esta prueba se presentaron instantes de tiempo en los cuales los marcadores 1 y/o 2 podían ser observados únicamente por una cámara, por esta razón no era posible realizar su reconstrucción al no tener suficiente información. Esto ocurrió debido a que en algunas posiciones el dispositivo queda de manera muy precisa entre los límites de grabación de la cámara y el ojo humano lo detecta en la grabación pero para el programa no es posible producto de las insuficientes condiciones de iluminación. Es por esto que es recomendable que el movimiento que se vaya a analizar, se realice dentro del espacio en el cual el sistema puede garantizar una adecuada iluminación.
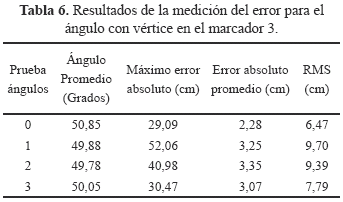
En la Tabla 6 se encuentran los resultados de la medición del error para el ángulo entre los marcadores 1, 2 y 3, con vértice en el marcador 3 (Fig. 10).
En los resultados de [4] el máximo RMS fue de 4,498 para el sistema Qualisys y el máximo error absoluto fue 14,309 grados para Elite. El resultado obtenido por el sistema CineMED II se debe a que el marcador 3 en algunos instantes de tiempo no es capturado por ninguna de las cámaras y por esta razón no se posible reconstruirlo. En el momento de calcular el ángulo no hay información para algún marcador y es por esta razón los errores son tan significativos.
En la Tabla 7 muestran los resultados obtenidos de la medición del error para la posición del marcador 7 (Fig. 10).
Esta prueba se realizó con el fin de evaluar la resolución del sistema en el momento en el que las trayectorias de dos marcadores diferentes se crucen. Es evidente que el sistema a pesar de requerir la intervención del usuario cuando el sistema no es capaz de definir que trayectoria pertenece a que marcador, sigue presentando problemas para realizar la reconstrucción correctamente. Para esto se decidió implementar una nueva intervención del usuario, en la cual, si observa que hay trayectoria de marcadores atípicas, pueda dar clic manualmente sobre el marcador en cada una de las cámaras para los frames que se identifiquen como atípicos.
3.3. Prueba piloto de un gesto de marcha humana:
Posteriormente al procesamiento de la prueba de marcha realizada sobre el sujeto de prueba por medio de CineMED II se pudo obtener inicialmente la reconstrucción tridimensional como se observa en la fig. 12. Los marcadores que presentan mayor inconveniente son los correspondientes al calcáneo distal y al maléolo lateral, dada su cercanía durante el gesto, que a veces hace que el sistema los detecte como uno sólo, para esto se implementó en CineMED una opción de corrección de trayectorias donde se puede seleccionar en un frame especifico la posición correcta del marcador que no se detectó adecuadamente. Una vez corroborado que la reconstrucción tridimensional es la deseada, se procede a aplicar el modelo cinemático para calcular los diferentes parámetros temporal-espaciales de la marcha, así como también los diferentes ángulos articulares durante el gesto de la marcha.
IV. CONCLUSIÓN
Cada una de las pruebas realizadas evalúa una característica que es relevante para los sistemas de análisis de movimiento. Los resultados generales demuestran que el sistema posee un desempeño muy cercano al de los sistemas comerciales, salvo en algunos casos especiales que se mencionan a continuación. A partir de la prueba estática se puede determinar que el sistema no tiene problemas en la reconstrucción de puntos ubicados estáticamente dentro del espacio de captura del sistema (Tabla 1).
Con base en los resultados de la prueba dos es posible afirmar que el sistema posee un buen desempeño cuando se le compara con los sistemas comerciales, solo siendo superado en exactitud por el sistema de la casa comercial Elite. En cada uno de los planos evaluados para la barra horizontal, sagital y vertical la media de los errores absolutos está por debajo de los 2 mm. Si consideramos que los marcadores que menor rango de movimiento en dirección vertical tienen, son los ubicados en las espinas iliacas y que su rango de movimiento es de alrededor de 30-50 cm dependiendo de la persona, esto se traduce en que el porcentaje de error del sistema para la medidas de menor rango es de aproximadamente 0,33-0,55%, lo cual es un error pequeño en comparación con el rango de movimiento de las medidas y el plano que requiere de mayor precisión.
Con respecto a la prueba que evaluaba varios de los factores importantes para un sistema de análisis de movimiento con la ayuda de un dispositivo especial, se encontró que el software automáticamente no proporciona total confiabilidad cuando los marcadores cruzan sus trayectorias. Esto más que ser un problema producto del algoritmo implementado, es un problema producto de las limitaciones de hardware que posee el sistema de captura, es decir, la imposibilidad de reconstruir el marcador en muchos de estos casos es debido a que solo se cuentan con cuatro cámaras para el proceso de reconstrucción, esto hace que el sistema no sea redundante y se den en muchos casos ambigüedades, producto de la poca información disponible de los marcadores, sobre todo cuando se analizan movimientos complejos (Tabla 5, 6 y 7). Estos problemas descritos anteriormente pueden ser solucionados agregando más cámaras al sistema o pidiendo la intervención del usuario en casos donde se presente esta ambigüedad, esta última opción será implementada como un trabajo futuro del sistema. Por otra parte las medidas de exactitud cuando no se presentan cruces de trayectorias u oclusiones muy prolongadas dieron resultados satisfactorios cuando se le comparan con sistema comerciales (Tabla 4).
Finalmente, durante la prueba de marcha del sistema se logró reconstruir la trayectoria de cada uno de los marcadores, sin embargo se presentaron algunos problemas de ambigüedad que requirieron la intervención del usuario, con el fin de corregir la trayectoria errónea de los marcadores.
AGRADECIMIENTO
Este proyecto ha sido financiado por Colciencias por la convocatoria 420 de problemas prioritarios de salud de 2006.
REFERENCIAS
[1] Herda L., Fua P., Plankers R., Boulic R. Using skeleton-based tracking to increase the reliability of optical motion capture. Human movement science, 20(3), 313-341, 2001. [ Links ]
[2] He J., Tian C. A statistical smoothness measure to eliminate outliers in motion trajectory tracking. Human movement science, 17(2), 189-200(12), April 1998. [ Links ]
[3] Heikkila J. Update calibration of a photogrammetric station. Close-Range Photogrammetry Meets Machine Vision, SPIE Proceedings, 1395, 1234, 1990. [ Links ]
[4] Whittle M.W. Clinical gait analysis: A review. Human movement science, 15, 369-387, 1996. [ Links ]
[5] Garrido J.L., Medina-Carnicer R., Martinez A. Design and evaluation of a new three-dimensional motion capture system based on video. Gait and posture, 24(1), 126-129, 2006. [ Links ]
[6] Cappozzo A., Croce U.D., Leardini A., Chiari L. Human movement analysis using stereophotogrammetry Part 1: theoretical background. Gait and posture, 21, 186-196, 2005. [ Links ]
[7] Richards J.G. The measurement of human motion: a comparison of commercially available systems. Human movement science, 18(5), 589-602, 1999. [ Links ]
[8] Ehara Y., Fujimoto H., Miyazaki S., Mochimaru M., Tanaka S., Yamamoto S. Comparison of the performance of 3D camera systems II. Gait and posture, 5(3), 251-255, 1997. [ Links ]
[9] Braidot A., Gallardo D.G., Spinetto J.I. Laboratoria de Biomecánica de bajo costo: desarrollo de sistema de videografía digita. Memorias XVII Congreso Brasileiro de Engenharia Biomédica, Brazil, 2000. [ Links ]
[10] Borghese N.A., Ferrigno G. An algorithm for 3D automatic movement detection by means of standard TV cameras. IEEE Transactions on biomedical engineering, 37(12), 1221-1223, 1990. [ Links ]
[11] Willneff J. 3D Particle tracking velocimetry based on image and object space information. Institute of Geodesy and Photogrammetry, Swiss Federal Institute of technology. 2002. Consultado el 13 de Julio en: http://www.photogrammetry.ethz.ch/research/ptv/corfu2002.pdf. [ Links ]
[12] Faugeras O., Robert L. What can two images tell us about a third one. International Journal of Computer vision, 18(1), 485-492, 1996. [ Links ]
[13] He J., Chun-Xiang T. A statistical smoothness measure to eliminate outliers in motion trajectory tracking. Human movement science. 17, 189-200, 1998. [ Links ]
[14] Abdel-Aziz Y.I., Karara H.M. Direct linear transformation from comparator coordinates into object space coordinates in closerange photogrammetry. Proceedings of the symposium on closerange photogrammetry, Falls Church, VA: American Society of Photogrammetry, 1971. [ Links ]
[15] Abdel-Aziz Y.I., Karara H.M. Direct linear transformation from comparator coordinates into object space coordinates in closerange photogrammetry. Proceedings of the ASP/UI symposium on close-range photogrammetry, 1978. [ Links ]
[16] Ji Q., Costa M., Haralick R. y Shaphiro L. A robust linear leastsquares estimation of camera exterior orientation using multiple geometric features. ISPRS Journal of photogrammetry and remote sensing, 55, 75-93, 2000. [ Links ]
[17] Ian A. F. Stokes, Paul Allard. Three-Dimensional Analysis of Human Movement. [ Links ]
[18] Watkins D. Fundamentals of Matrix computations. John Wiley and Sons, Inc, 1991. [ Links ]
[19] Kadaba M.P., Ramakrishnan H.K., Wootten M.E. Measurement of lower extremity kinematics during level walking. Journal of orthopaedic research, 8, 383-392, 1997. [ Links ]
[20] Vaughan C., Davis B., O'Connor J. Dynamics of human gait. Ed. Kiboho Publishers, 2003. Capítulo 3, 15-43. [ Links ]