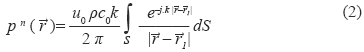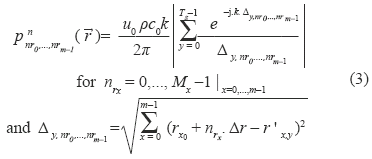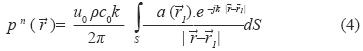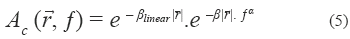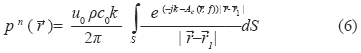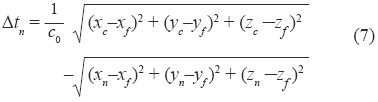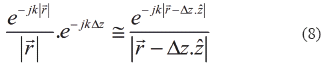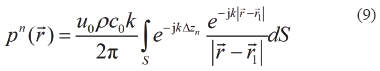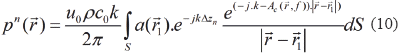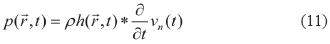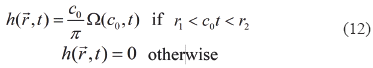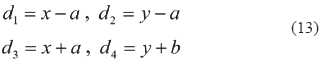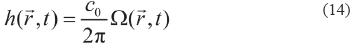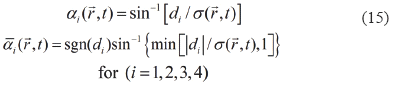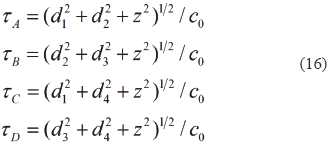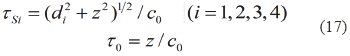Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Ingeniería Biomédica
Print version ISSN 1909-9762
Rev. ing. biomed. vol.7 no.13 Medellín Jan./June 2013
DEVELOPMENT OF A MATLAB ENVIRONMENT SOFTWARE FOR SIMULATION OF ULTRASONIC FIELD
DESARROLLO DE UN SOFTWARE EN MATLAB PARA LA SIMULACIÓN DE CAMPO ULTRASÓNICO
Reynaldo Tronco Gasparini1,2, Vera Lúcia da Silveira Nantes Button1
1 Biomedical Engineering Department, School of Electrical and Computing Engineering, UNICAMP, Campinas, Brazil.
2 Dirección para correspondencia: reynaldogasp@yahoo.com.br.
Recibido 30 de enero de 2013. Aprobado 29 de julio de 2013
ABSTRACT
The study of the acoustic field generated by an ultrasonic transducer is fundamental to its construction and characterization, because it defines how it will behave before being built. It also defines whether it is feasible or not, for the application to which it was designed. It can also lead to modifications to the project so it behaves as expected. In this work, a software was implemented in MATLAB®, for computational simulation of acoustic fields generated by ultrasonic transducers of different configurations. Two models were used, Zemanek and Stepanishen. Transducers with focus and apodization and transmission medium with attenuation may also be simulated. For the simulation of Zemanek's model, the mathematical method of discretization was used. The Stepanishen's model used an analytical solution for the impulse response. The developed programs were aggregated into a computer package, named FSIM, and a graphic interface was created. The user can choose among some of the transducer configurations and simulation parameters already implemented. FSIM has a modular architecture and allows further simulation modules to be added. The simulations were validated comparing results to those previously published in classical papers from Zemanek, and from Lockwood and Willete, in addition to prior results from research studies conducted at the Biomedical Engineering Department of the School of Electrical and Computing Engineering at the Universidade Estadual de Campinas (UNICAMP).
KEY WORDS: Acoustic Field Simulation, Discrete Representation, Impulse Response, MATLAB, Ultrasound Transducers.
RESUMEN
El estudio del campo acústico generado por un transductor ultrasónico es fundamental para su construcción y caracterización, ya que define cómo se comportará antes de ser construido. También define si realmente es factible para la aplicación a la que fue diseñado, y también puede sugerir modificaciones al proyecto, para que se comporte como se espera. En este trabajo un software fue implementado en MATLAB®, para la simulación computacional de los campos acústicos generados por los transductores ultrasónicos de diferentes configuraciones. Dos modelos fueran usados, Zemanek y Stepanishen. Transductores con el enfoque y apodización y medios con atenuación también pueden ser simulados. Para la simulación del modelo de Zemanek, se utilizó el método matemático de discretización y para el modelo de Stepanishen, se empleó una solución analítica para la respuesta impulsiva. Los programas desarrollados fueron agregados en un paquete computacional, llamado FSIM, y una interfaz gráfica fue creada. El usuario puede elegir entre algunas configuraciones del transductor y parámetros de simulación ya implementados; FSIM tiene una arquitectura modular y permite que otros módulos de simulación sean añadidos. Las simulaciones fueron validadas comparando resultados obtenidos previamente por otros trabajos de investigación del Departamento de Ingeniería Biomédica de la Facultad de Ingeniería Eléctrica y Computación de la UNICAMP y por los artículos clásicos de Zemanek y Lockwood y Willette.
PALABRAS CLAVE: MATLAB, Representación Discreta, Respuesta Impulsiva, Simulación del Campo Acústico, Transductores de Ultrasonido.
I. INTRODUCTION
Ultrasonic waves are mechanical waves with vibration frequency above the audible range (20 Hz - 20 KHz) and propagate in any medium (water, blood, air, biological tissue, etc.). Each material has characteristics acoustic properties as propagation speed, attenuation and acoustic impedance.
In an ultrasound equipment, the transducer is responsible for transforming the electrical pulses generated by the equipment in acoustic waves which will propagate through the medium (biological tissue). The transducer is also responsible for receiving the echoes from the pulses emitted and turn them into electrical signals that will be processed to reconstruct the medium image.
The characterization and modeling of the transducers acoustic field is fundamental for interpretation of the signals, since it represents the interaction between the waves they produce and the medium in which these waves are propagated.
The understanding of the acoustic field generated by an ultrasonic transducer according to their characteristics, can guide its construction and characterization, indicating whether it is really feasible or not, for the application to which it was designed. It can also suggest modifications to the project so it behaves as expected [1].
The field modeling consists in determining the acoustic pressure at a set of points in space applied to the transducer surface, either by analytical equations, where numerical integration and convolution are employed, or by numerical approach [2]. This modeling can be performed using mathematical models and computer simulation.
Acoustic field modeling has been widely studied since the sixties. But, it was in the nineteenth century, when Lord Rayleigh developed equations that describe the acoustic wave propagation phenomena. Zemanek developed a numerical method for calculating the acoustic field of a circular transducer [3]. Stepanishen developed one of the most used models today, the impulse response method [4, 5]. Piwakowski and Delannoy (1989) described the discrete representation method for calculating the acoustic field for any transducer geometry [6]. Lockwood and Willete developed a method for calculating an analytical solution for the acoustic field of rectangular transducers [7]. San Emeterio and Ullate (1992) gave exact expressions for the velocity potential impulse response of rectangular transducers [8]. Since 1996, Jensen has published several papers related to the software Field II, considered the gold standard program for acoustic field simulation. This program is considered very flexible since it allows the simulation of any excitation signal and transducer geometry [9].
In this work we describe a software, named FSIM, with graphical interface, implemented in MATLAB® for the simulation of acoustic fields generated by ultrasound transducers of different configurations, using two models, Zemanek [3] and Stepanishen [4, 5]. Transducers with focusing and apodization and transmission medium with attenuation may also be simulated. Simulation results are displayed in several graphical templates. The purpose of this software is to support transducer development projects, allowing the prediction of the acoustic field behavior before transducer construction.
II. MATERIALS AND METHODS
A. Zemanek's model simulation
For this model, the Discrete Representation Method (DRM) was employed. This approach tends to the analytical solution. It consists in the domain discretization, i.e., the division of the integration area in a finite number of points, turning the continuous domain into a discrete one.
The accuracy of the results is only limited by the number of elements adopted for modeling the field and the transducer face [6]. The higher the discretization (sampling) is, the greater the accuracy of the simulated field.
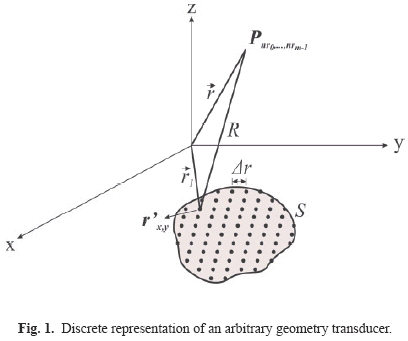
The evaluation of the acoustic field using this method is performed discretizing the space in three dimensions (applying rectangular coordinates) into a finite number of points, using sufficient samples to limit quantization errors and to satisfy the Nyquist theorem. For that, a spatial resolution of at least half wavelength (λ/2) of the excitation signal is adopted [10]. Then, the transducer face is discretized in many active area elements, and the resulting sound pressure at a point in space will be the sum of the individual contribution of each of these elements.
An advantage of Zemanek's model is that it considers uniform motion all over the transducer face, turning the piston velocity in a continuous function and, thus, it is restricted to fields generated by transducers in continuous excitation. Considering this case, the piston velocity is:
where u0 is the peak amplitude of the transducer velocity, t is the time, ω is the angular velocity and j is the complex operator. The normalized acoustic pressure pn (r) at a point in space is [3]:
where, ρ is the acoustic medium density, c0 the sound speed, k the wave number, 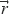 the position vector of a point in space,
the position vector of a point in space, 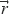 1 the position vector of the piston active element and S is the piston active area.
1 the position vector of the piston active element and S is the piston active area.
Rewriting (2) in its discrete form:
where pnnr0,...,nrm-1 corresponds to the acoustic field normalized pressure between 0 and 1 in the nrx-th sample of the x-th field spatial dimension, is the distance between the nrx-th field spatial sample to the transducer active element r'x,y, which represents the position of the y-th transducer active element (Ts elements) in the x-th spatial dimension. It is given by r'x,y = rx0 + y. Δrx, where rx0 is the initial sample and Δrx is the sample rate of the x-th spatial dimension, and m is the number of spatial dimensions. Fig. 1 shows a transducer discrete representation.
Apodization - it is the non-uniform polarization of piezoelectric transducer elements, i.e., when the polarization intensity and direction change over the piezoelectric element. It aims to establish a spatial distribution of the active elements of the transducer face, in order to minimize the contribution of the vibration, generated by the edge region in the ultrasonic field, resulting in acoustic diffraction [11].
The apodization results in the reduction of side lobes and the generation of a uniform ultrasonic field. Apodization a(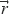 1,t) can be inserted in (2). Considering only single element transducer and uniform motion all over the transducer face, only constant apodization is considered too, i.e., a(
1,t) can be inserted in (2). Considering only single element transducer and uniform motion all over the transducer face, only constant apodization is considered too, i.e., a(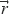 1,t) = a(
1,t) = a(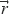 1) , and (2) can be written as [12]:
1) , and (2) can be written as [12]:
where a(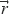 1) defines the gain of each transducer active element in
1) defines the gain of each transducer active element in 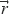 1.
1.
Apodization is defined by MATLAB® masks (windows), originally used in signal processing. Some of the windows implemented in the program are: Hanning, Bartlett, Blackman, Triang, Kaiser and Hamming [13].
Attenuation - acoustic wave attenuation occurs due to the diminution in the pressure variation amplitude that decreases exponentially as a function of distance. Several mechanisms may produce attenuation, including absorption and dispersion.
Attenuation effects can be modeled by dividing the attenuation in one dependent and other independent term of frequency [12]:
where βlinear and β are the frequency-independent, in dB/cm, and frequency-dependent attenuation coefficient, in dB/(cm·MHz), respectively, α is the dependence between attenuation and frequency, and Ac (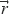 , f) is the attenuation in dB.
, f) is the attenuation in dB.
Focusing - aims to align the pressure field originated from all over the piston face to reach a particular point in space at the same time. This process can be obtained using curved surface transducers, overlapping lenses over the piston or applying time delay in the excitation of array transducers elements.
For computational simulation, focus can be represented by an advance on the position of the z-axis active element Δzn=c0.Δtn.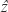 [10], given by [12]:
[10], given by [12]:
where (xf, yf, zf) = rf is the focal point, (xn, yn, zn) is the center of the n element, (xc, yc, zc) is the reference center point and tn is the propagation time.
For the particular case of farfield simulation [10]:
Then:
Finally, the equation that describes Zemanek's model considering apodization, attenuation and focus functions is:
B. Stepanishen's model simulation
Stepanishen [4, 5] proposed an analytical solution for the acoustic field defining the impulse response function h(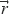 , t) for each transducer geometry, circular and rectangular. After finding the impulse response function, the piston velocity function is determined and its temporal derivative is calculated. The medium density multiplied by the convolution of these two functions corresponds to the acoustic field pressure at a point of interest.
, t) for each transducer geometry, circular and rectangular. After finding the impulse response function, the piston velocity function is determined and its temporal derivative is calculated. The medium density multiplied by the convolution of these two functions corresponds to the acoustic field pressure at a point of interest.
The acoustic field pressure is:
where t is the time, h(r ,t) is the transducer impulse response, 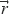 = (x, y, z) the position vector of a point in space and vn(t) is the transducer active element velocity.
= (x, y, z) the position vector of a point in space and vn(t) is the transducer active element velocity.
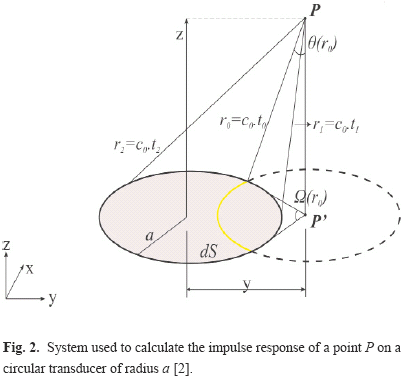
For the particular case of a circular flat transducer, Stepanishen approach [4, 5] was used to determine an analytical solution for the impulse response. Due to the piston radial symmetry, it is easier to be found. It can be computed defining expressions for arc angles formed in the piston surface Ω(r0) for two projected geometric regions (internal and external) shown in Fig. 2.
where r1 e r2 represent the piston closest edge and farthest edge distances to the spatial point of interest. Table 1 shows expressions to compute the impulse response of circular transducers in both regions of interest.
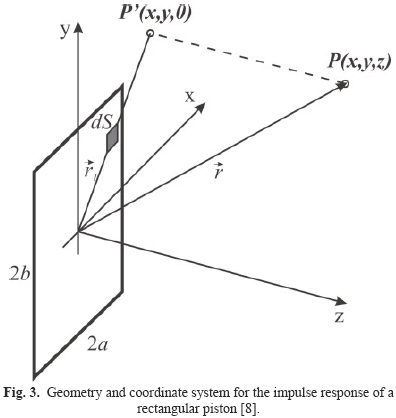
The determination of the impulse response function of the rectangular transducer is more complicated than the circular one. San Emeterio and Ullate [8] obtained an exact analytical solution for the impulse response that is used to calculate the sound field pressure of a rectangular transducer.
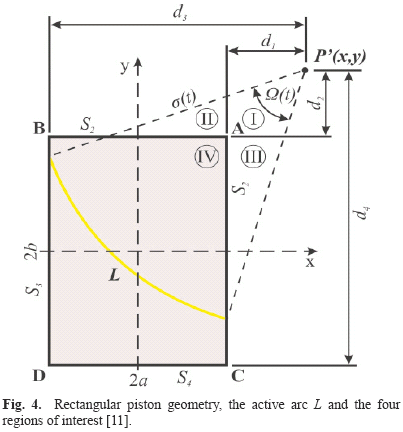
Considering a rectangular transducer of 2a wide and 2b long, sorrounded by a rigid baffle and located at z = 0 plane (Fig. 3), only points in the x ≥ 0 and y ≥ 0 quadrant is considered. The rectangles sides are named Si (i = 1 - 4) and distances between the field point projection P' to the straight lines, which contain the rectangle sides |di|(i = 1 - 4) are:
There isn't only one equation to describe the angle Ω(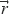 , t) and analytical expressions have to be obtained by dividing x ≥ 0 and y ≥ 0 quadrant in four regions: region I: x ≥ a and y ≥ b; region II: x ≤ a and y ≥ b; region III: x ≥ a and y ≤ b; region IV: x ≤ a and y ≤ b, as shown in Fig. 4.
, t) and analytical expressions have to be obtained by dividing x ≥ 0 and y ≥ 0 quadrant in four regions: region I: x ≥ a and y ≥ b; region II: x ≤ a and y ≥ b; region III: x ≥ a and y ≤ b; region IV: x ≤ a and y ≤ b, as shown in Fig. 4.
The impulse response of a rigid piston is determined by:
where Ω(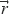 ,t) is the arc angle formed by the circumference aperture centered in P' intercepted by the rectangular piston edges. These arc angles values are calculated by San Emeterio e Ullate [8] for each of the mentioned regions and are shown in Table 2.
,t) is the arc angle formed by the circumference aperture centered in P' intercepted by the rectangular piston edges. These arc angles values are calculated by San Emeterio e Ullate [8] for each of the mentioned regions and are shown in Table 2.
The values of αi e 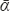 i in Table 2 are:
i in Table 2 are:
where sgn(x) is equal to 1 if x is positive and -1 if x is negative and σ(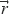 ,t) = (c02t2-z2)½. The transit times of the signal between the vertices A, B, C and D to the point P(
,t) = (c02t2-z2)½. The transit times of the signal between the vertices A, B, C and D to the point P(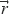 ) are:
) are:
The time instant τSi when the active arcs become tangent to the rectangle sides Si and the time τ0 for the plane wave reach the point P(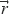 ) are:
) are:
The impulse response h(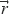 ,t) is delimited by the time interval (τmin,, τD), and outside this limits h(
,t) is delimited by the time interval (τmin,, τD), and outside this limits h(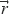 ,t) = 0. The minimal time τmin is equal to τA, τS2, τS1 or τ0 for field points in the regions I, II, III and IV, respectively.
,t) = 0. The minimal time τmin is equal to τA, τS2, τS1 or τ0 for field points in the regions I, II, III and IV, respectively.
After defining the angle Ω(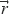 ,t), this is substituted in (14) to find the transducer impulse response. The acoustic field pressure, likewise the circular piston, is obtained by the convolution between the impulse response function and the velocity derivative at a point in space.
,t), this is substituted in (14) to find the transducer impulse response. The acoustic field pressure, likewise the circular piston, is obtained by the convolution between the impulse response function and the velocity derivative at a point in space.
C. Software Development
In this software, named FSIM, a graphical interface was developed to facilitate the interaction between user and program, where the transducer main characteristics and the acoustic field parameters can be inserted. They are:
- transducer geometry and dimensions;
- focusing in x, y and z axes, in mm;
- resolution, assuming integer values between 1 and 6 (corresponding to values between λ/2 and λ/12);
- transducer apodization,
- sound speed in acoustic medium in m/s;
- vibration frequency of the transducer face in Hz;
- acoustic medium attenuation using values of βlinear, β and α;
- graphic dimensions in mm;
- five graphic templates for simulation: 3D pressure xy plane, xz plane, 3D slice, 2D pressure z-axis and pressure peak contour. All graphics show normalized pressure values between 0 and 1.
D. Hardware and Software
The program and simulations were performed using an Intel® CoreTM Quad Q8200, 2.33 GHz, 4 Gb of RAM Memory and 32 bits Windows 7. Both simulation methods and graphical interface of the FSIM were implemented in MATLAB®, MathWorks Inc. R2009a (version 7.8.0.347).
III. RESULTS
This section presents the FSIM graphical interface and simulations obtained using the software. In the home screen (Fig. 5), input values and the graphic template for the simulation are defined. The program has some preset input values, which can be changed. Default values include the sound speed of the medium, attenuation values and the acoustic field dimensions.
Applying Zemanek's model, some of the simulated transducers were:
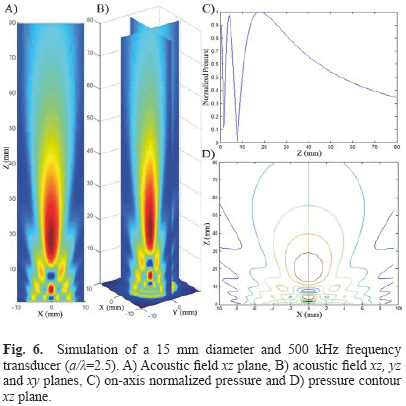
1. Circular piston of 15 mm diameter and 500 kHz frequency (a/λ=2.5) (Fig. 6);
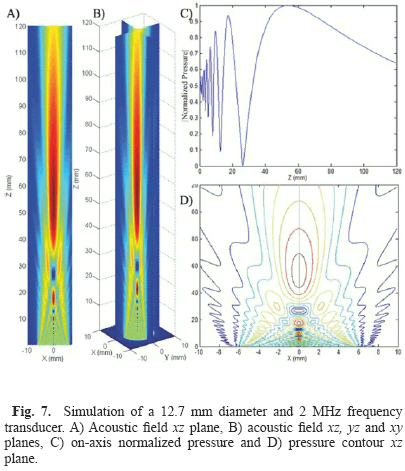
2. Circular piston of 12.7 mm diameter and 2 MHz frequency (Fig. 7);
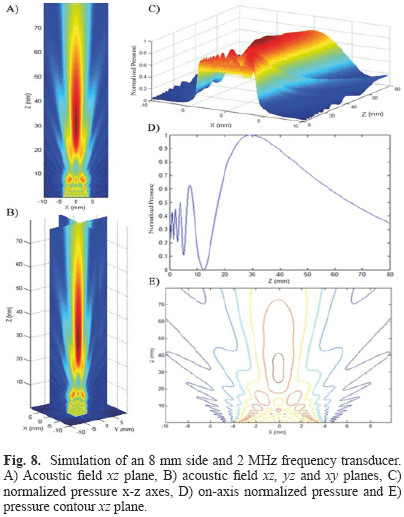
3. Square piston of 8 mm side, 2 MHz frequency (Fig. 8);
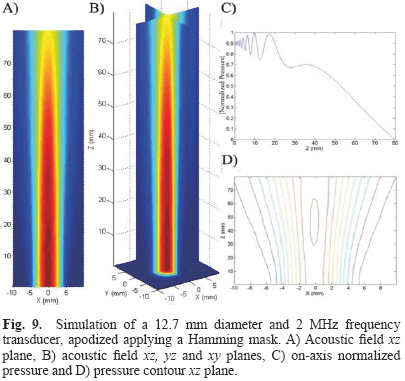
4. Circular transducer of 12.7 mm diameter 2 MHz frequency, apodized applying a Hamming mask (Fig. 9);
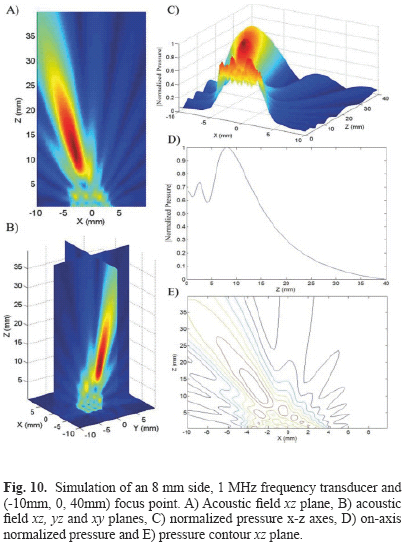
5. Square piston of 8 mm side, 1 MHz and (-10mm, 0, 40mm) focus point (Fig. 10);
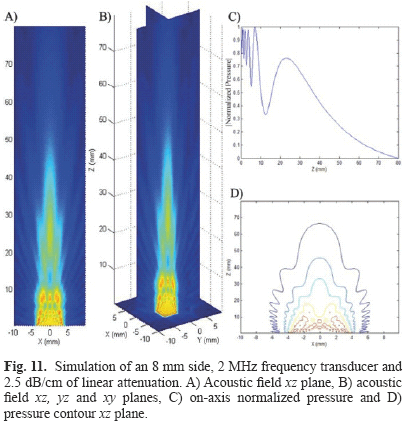
6. Square piston of 8 mm side, 2 MHz frequency and 2.5 dB/cm of linear attenuation (Fig. 11).
Applying Stepanishen's model, the simulated transducers were:
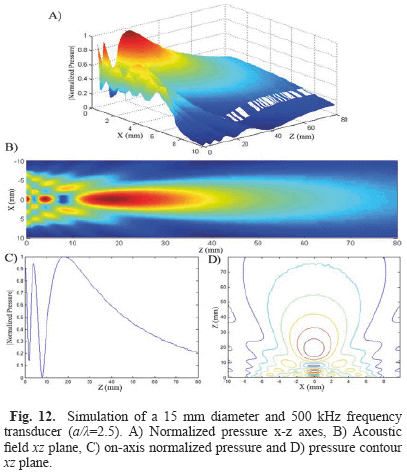
7. Circular transducer of 15 mm diameter and 500 kHz frequency (Fig. 12);
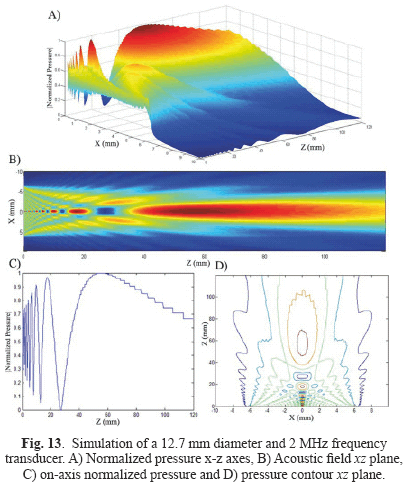
8. Circular transducer of 12.7 mm diameter and 2 MHz frequency (Fig. 13);
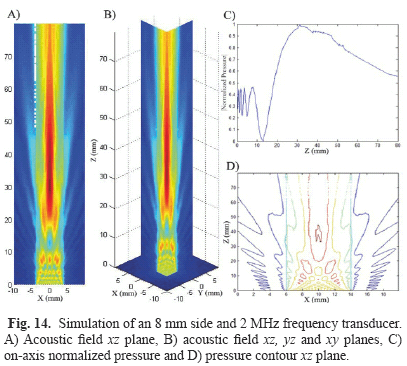
9. Square piston of 8 mm side, 2 MHz frequency (Fig. 14).
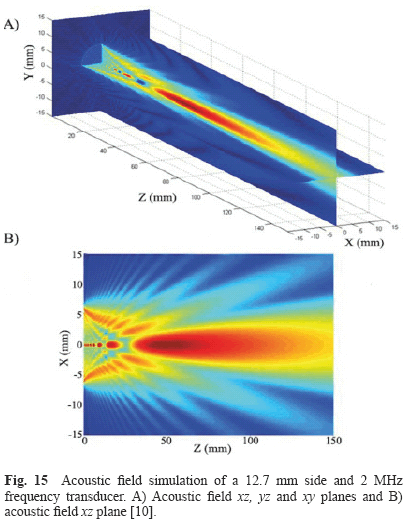
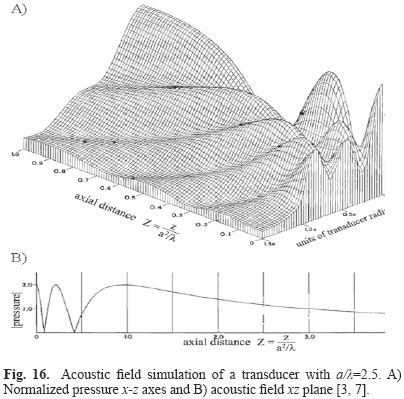
Fig. 15 and Fig. 16 show the simulations obtained by Albuquerque [10], Zemanek [3], Lockwood and Willette [7] and were used to validate the simulations performed by FSIM.
IV. DISCUSSION
Analyzing Zemanek's model algorithm Ni=Tx.Ty.Tz.Tsx.Tsy, and Stepanishen's one Ni=Tx.Ty.Tz.Δt for the rectangular piston and Ni=Tθ.Tz.Δt for the circular piston. Tx.Ty.Tz are space points in the x, y and z axes, respectively, Tsx.Tsy are transducer active area elements, Tθ.Tz is the total number of space points in cylindrical coordinates, Δt is the number of time samples defined empirically and Ni is the amount of iterations. As Stepanishen's model requires fewer iterations than Zemanek's one, the computational cost is lower. Nevertheless, due to the greater complexity of the analytical solution of the rectangular transducer impulse response, it executes more iterations than the circular one and, hence, requires greater processing time.
FSIM simulations were compared and analyzed qualitatively and they are in agreement with those obtained by Nicacio [1] and Albuquerque [10] works, Zemanek [3] and Lockwood and Willette [7] classical papers. Indeed, it is possible to observe the well-known properties of acoustic fields such as the interaction between plane and edge waves in the nearfield region and the transition from the nearfield to the farfield region. The uniform nearfield due to apodization functions, the change of the acoustic field steering when a focus point is determined and the diminution of the acoustic field intensity when attenuation is applied can also be observed.
Other programs for acoustic field simulation already exist such as Field II, which is the gold standard software, but it has a different purpose. Instead of allowing more complex acoustic field simulation applying only one model like Field II [9], FSIM allows simpler simulations applying different models and other models can be added to the program.
Analyzing both models, Stepanishen is more complete than Zemanek's one and requires less iterations. However, Zemanek is more accurate, because it does not have the "noise" found in Stepanishen results, since time discretization is not necessary. Even when the resolution is increased, the noise is not eliminated, and it only approximates one point to another. Another characteristic observed in the Stepanishen's simulations is the presence of "stairs" in the farfield region. This may occur due to numerical approximations and small variations between points, amplified due to the magnitude of these numbers, stored by the computer in a floating-point form [1]. Wu, Kazys and Stepinski [14, 15] discuss the presence of noise in the numerical implementation of the angular spectrum approach, which can arise by three types of artifact: frequency aliasing, half-sample length phase shift and spatial aliasing.
The DRM was very effective to simulate acoustic field and its precision is limited only by the resolution, which depends on the transducer frequency. The larger the transducer and the field dimension, more points are defined where the acoustic field is computed, likewise the higher the resolution or the transducer frequency is, the higher the discretization and, thus, is the processing time to perform the simulations. The method used by the program becomes unfeasible for very high frequency transducer simulation and if real time simulation is necessary. This is the major limitation of the FSIM. Table 3 shows the processing time of some simulations.
V. CONCLUSION
FSIM program has proved to be a useful and efficient tool for studying and understanding the acoustic field behavior generated by ultrasonic transducers. Its friendly interface makes it an easy program to handle, which is its major advantage, if compared to other simulation programs. The software can help transducers designers, predicting the acoustic field generated by transducers before their construction; furthermore, the program code is accessible and can be complemented with other transducers models and functions. This program is already available to be used by undergraduate and graduate students and researchers of the Biomedical Engineering Department of the School of Electrical and Computing Engineering of UNICAMP.
REFERENCES
[1]. Nicacio, H. Simulação e Mapeamento de Campos Ultra-sônicos para Caracterização de Transdutores Utilizando os Métodos Pontual e Angular. MSc Thesis, Masters of Biomedical Engineering, FEEC/UNICAMP, 2002. [ Links ]
[2]. Formigoni, P. O. Modelagem de Ondas Ultrassônicas Refletidas por Superfícies de Geometrias Diversas. MSc Thesis, Masters in Engineering, USP, 2011. [ Links ]
[3]. Zemanek, J. Beam Behavior within the Nearfield of a Vibrating Piston. Journal of Acoustical Society of America, 49, 1 (part 2), 181-191, 1970. [ Links ]
[4]. Stepanishen, P. R. The Time-Dependent Force and Radiation Impedance on a Piston in a Rigid Infinite Planar Baffle. Journal of Acoustical Society of America, 49, 3, 841-849, 1970. [ Links ]
[5]. Stepanishen, P. R. Transient Radiation from Pistons in an Infinite Plane Baffle. Journal of Acoustical Society of America, 69, 5, 1629-1638, 1970. [ Links ]
[6]. Piwakowski, B.; Delannoy, B. Method for Computing Spatial Pulse Response: Time-domain Approach. Journal of Acoustical Society of America, 86, 6, 2422-2432, 1989. [ Links ]
[7]. Lockwood, J.C.; Willette, J.G. High-Speed Method for Computing the Exact Solution for the Pressure Variations in the Nearfield of a Baffled Piston. Journal of Acoustical Society of America, 53, 3, 735-741, 1973. [ Links ]
[8]. San Emeterio, J. L.; Ullate, L. G. Diffraction Impulse Response of Rectangular Piston. Journal of Acoustical Society of America, 92, 2, 651-662, 1992. [ Links ]
[9]. Jensen, J. A. Field: A Program for Simulating Ultrasound Systems. Medical & Biological Engineering & Computing, 34, n. 1, 351-353, 1996. [ Links ]
[10]. Albuquerque, J. A. G. Sistema Computacional para Simulação e Processamento de Imagens Ultra-sônicas. Doctorate Thesis, Doctorate in Biomedical Engineering, FEEC/UNICAMP, 2006. [ Links ]
[11]. Button, V. L. S. N. Efeitos da Polarização Não-uniforme de Cerâmicas Piezelétricas no Campo de Transdutores de Ultra-som, Doctorate Thesis, Doctorate in Biomedical Engineering, FEEC/ UNICAMP, 1998. [ Links ]
[12]. Jensen, J. A. Ultrasound Imaging and Its Modeling, In: Imaging of Complex Media with Acoustic and Seismic Waves, Ed. Fink, M. et al, 135-164, 2002. [ Links ]
[13]. Oppenheim, A. V, Schafer, R. W. Discrete-time Signal Processing, Prentice-Hall, Inc., 1999. [ Links ]
[14]. Wu, P.; Kazys, R.; Stepinski, T. Analysis of the Numerically Implemented Angular Spectrum Approach Based on the Evaluation of Two-dimensional Acoustic Fields. Part I. Errors Due to the Discrete Fourier Transform and Discretization. Journal of Acoustical Society of America, 99, 3, 1339-1348, 1996. [ Links ]
[15]. Wu, P.; Kazys, R.; Stepinski, T. Analysis of the Numerically Implemented Angular Spectrum Approach Based on the Evaluation of Two-dimensional Acoustic Fields. Part II. Characteristics as a Function of Angular Range. Journal of Acoustical Society of America, 99, 3, 1349-1359, 1996. [ Links ]