1. Introducción
En los últimos años ha crecido el interés por indagar acerca de las creencias que tienen, tanto docentes en formación y en servicio como los estudiantes de educación básica y media, acerca de las matemáticas (Campos, 2008; Cross, 2015; Kislenko, Breiteig & Grevholm, 2005; Vesga & Falk, 2016; 2018; Vizcaíno & Otero, 2015). Algunos estudios evidencian que el aprendizaje de las matemáticas por parte de estudiantes de educación básica y media, está fuertemente ligado con sus creencias y actitudes acerca de lo que ellos consideran que son las matemáticas, (Chaves, Castillo & Gamboa, 2008; Kislenko et al., 2005; Lazim, Abu & Wong, 2004).
A partir de las experiencias vividas por los estudiantes en el proceso de aprendizaje, éstos tienen reacciones, actitudes y comportamientos, que son catalogados como parte del factor afectivo de sus creencias e influyen en la forma como se enfrentan a diferentes situaciones de aprendizaje de las matemáticas (Campos, 2008; Vizcaíno et al., 2015). El docente es el encargado de proponer actividades, diseñar materiales, hacer aportes y modificaciones al currículo, y liderar diferentes dinámicas y didácticas que se desarrollan en clase; esto hace que pueda afectar de manera directa las creencias en los estudiantes, influenciado por las propias, y hacer que se favorezca o desmejore el aprendizaje de las matemáticas, así como el gusto e interés por las mismas (Chaves et al., 2008; Vizcaíno et al., 2015).
Igualmente, se sabe que a partir de la resolución de problemas se puede llevar a los estudiantes a la construcción de creencias positivas hacia las matemáticas (McLeod, 1988; Callejo & Vila, 2003). La investigación de McLeod (1988), confirma que es posible afectar las creencias que tienen los estudiantes sobre las matemáticas, con base en un trabajo basado en la resolución de problemas. El autor señala que pudo evidenciar diferentes reacciones afectivas y emocionales que tienen los estudiantes al enfrentarse a un problema en la búsqueda de su solución, lo que repercute directamente sobre la percepción que tienen acerca de las matemáticas. Asimismo, al combinar diferentes experiencias a lo largo del proceso de enseñanza aprendizaje de las matemáticas, los estudiantes pueden cambiar su autoconcepto frente al aprendizaje, sentirse más participativos y comprometidos y esto puede incluso reflejarse en su rendimiento académico (McLeod, 1988; Gutiérrez-Rodríguez, 2018).
En esta investigación se diseñó una propuesta didáctica, basada en problemas no rutinarios para ver el efecto que tenía en las creencias sobre la matemática, en un grupo de estudiantes de séptimo grado de una institución de carácter oficial. A continuación, se presenta el referente teórico y la metodología empleada en el estudio, junto con los principales resultados y conclusiones.
2. Marco teórico y método
2.1 Fundamento teórico
Instrumentos para aproximarse a las creencias
Una línea de investigación en este marco se deriva de los trabajos realizados por Schommer (1990) desde la década de los noventa, quien planteó una aproximación a las creencias epistemológicas de los estudiantes sobre las matemáticas, como un sistema conformado por cinco dimensiones, que están relacionadas ellas entre sí, pero no atadas con las demás y pueden variar, por lo que es un sistema independiente. Para cada dimensión, se describen las creencias de ingenuas a sofisticadas; además, dada la mirada multidimensional de las creencias, una persona puede tener al mismo tiempo unas creencias a un nivel sofisticado y otras a un nivel muy simple. En la tabla 1 se describe esta categorización.
Tabla 1 Creencias Epistemológicas sobre la matemática, modelo de Schommer (1990).
| Dimensión/creencias | No sofisticado | Sofisticado |
|---|---|---|
| Estabilidad del conocimiento | Cierto o incambiable | Tentativo |
| Estructura del conocimiento | Aislado. Piezas conectadas. Simple | Conceptos integrados |
| Fuente del conocimiento | Procedente de la autoridad | Procedente de la razón |
| Velocidad del aprendizaje | Rápido o no | Gradual |
| Habilidad para aprender | Habilidad innata | Improbable |
En la tabla 1, las primeras tres creencias están referidas a la naturaleza del conocimiento y las otras dos a la naturaleza del aprendizaje. La visión ingenua del conocimiento considera las matemáticas como una verdad que consiste en fragmentos aislados de conocimiento, que son transmitidos por la autoridad; mientras que una visión más sofisticada considera que el conocimiento es tentativo y evolutivo y consiste en conceptos interrelacionados que se construyen (Schommer, 1990).
Walker (2007), parte, entre otros, de los trabajos de Schommer (1990; 1994), diseñando y validando el Inventario de Creencias Epistemológicas, al que le incluye una dimensión denominada “aplicabilidad al mundo real”, que en una mirada ingenua considera no aplicabilidad hacia un nivel de sofisticación en el cual sí la hay. Con base en este trabajo Vizcaíno et al., (2015) diseñaron y validaron un instrumento para analizar las creencias epistemológicas sobre las matemáticas de estudiantes de educación básica y media, en el cual encontraron cuatro dimensiones: Habilidad Innata; Conocimiento Simple, Dependiente de la Autoridad; Conocimiento Relativo-Aprendizaje Adquirido; y, Aprendizaje Rápido e Inaplicable. Este último instrumento fue el utilizado en el desarrollo de la presente investigación.
Solución de problemas
Los trabajos e investigaciones de Polya (1965), muestran cómo ayudar a los estudiantes a pensar por sí mismos, a resolver problemas. Para ello, Polya se interesaba no sólo en la solución de problemas sino también en la forma como se puede llegar a la misma, buscando que los estudiantes comprendan los motivos y procesos que se deben tener en cuenta. Polya propone cuatro pasos ampliamente conocidos para la resolución de problemas: comprender el problema, concebir un plan, ejecutar el plan y examinar la solución obtenida.
Schoenfeld (1985), considera el trabajo realizado por Polya y señala cuatro enfoques que, a su parecer, marcan el trabajo sobre la resolución de problemas a nivel internacional. El primero hace referencia a los problemas presentados de forma escrita, los cuales sirven para mostrar las matemáticas de una forma muy sencilla pero que a su vez sirven para ubicarla dentro del mundo real. Un segundo enfoque hace referencia a la aplicación de las matemáticas al mundo real, en donde se muestra una faceta mucho más sofisticada de ella. En el tercer enfoque se hace énfasis en la relación del pensamiento matemático con los problemas un poco más complejos, mediante una exploración mucho más detallada, a partir de los procesos cognitivos de la mente en el estudiante. Por último, propone determinar los tipos de habilidades necesarias para resolver problemas matemáticos más complejos, para así desarrollarlas mediante los procesos de enseñanza.
Por otra parte, Mason, Burton y Stacey (1988) proponen una manera de abordar cualquier problema de forma eficaz, para lograr mayor aprendizaje y gusto por el trabajo en matemáticas. Para ello proponen un modelo para la resolución de problemas que tiene en cuenta la influencia del factor afectivo en el proceso de resolución de problemas, vinculando cinco aspectos importantes para lograrlo:
En primer lugar, atacar los problemas concienzudamente, es decir que los estudiantes pueden por sí mismos pensar matemáticamente. Segundo, reflexionar a partir de las experiencias acumuladas, ya que el razonamiento matemático puede mejorarse por la práctica unida a la reflexión. Tercero, conectar las impresiones recibidas con la acción, donde el razonamiento matemático viene motivado por una situación en la que se mezclan contradicción, tensión y sorpresa. Cuarto, estudiar cuidadosamente el proceso de resolución de los mismos problemas, donde el razonamiento matemático se mueve en una atmósfera cuyos ingredientes principales son pregunta, reto y reflexión. Y quinto, observar cómo encaja lo aprendido con la experiencia, para lo cual el razonamiento de tipo matemático ayudará al estudiante a entenderse mejor a sí mismo y al mundo que lo rodea.
En la presente investigación se tomó la propuesta de Mason, Burton y Stacey para la adaptación y aplicación de los problemas planteados.
2.2 Metodología
Se contó con la población de un colegio oficial de la ciudad de Bogotá (Colombia). La muestra fue de 24 estudiantes, 8 mujeres y 16 hombres. La edad de los estudiantes estaba entre 12 y 15 años, donde el 80% de ellos tenía 13 años. La implementación de las actividades se realizó en una clase regular de matemáticas, una vez a la semana, durante seis semanas seguidas.
Se adaptaron cinco actividades de resolución de problemas de Mason et al., (1988) para que los estudiantes pudieran explorar, particularizar, generalizar, conjeturar, comprobar y crear, y para que reflexionaran sobre la efectividad y utilidad de los procesos empleados. Cada actividad estaba conformada por dos partes: en la primera, los estudiantes trabajaban de forma individual, se hacía una aproximación a la situación planteada para garantizar su comprensión; en la segunda, para trabajo grupal (generalmente en parejas), los estudiantes buscaban patrones, hacían conjeturas y debían argumentar o no sobre la validez de las mismas, mediante el intercambio de ideas entre ellos y luego con la socialización a todo el grupo.
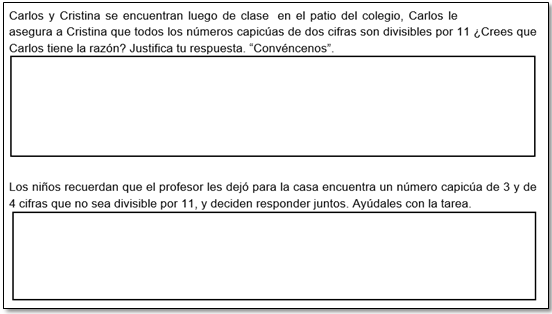
En la actividad 1, por ejemplo, denominada “Números capicúas”, en la primera parte se introduce el concepto, se verifica que sea comprendido y se pide a los estudiantes explorar con algunas propiedades que cumplen o no, como lo muestran las figuras 1 y 2.
En la segunda parte, luego de que los estudiantes socializan sus respuestas en la primera parte, se los va guiando para que puedan conjeturar y argumentar, como lo muestra la figura 3.
Al finalizar cada una de las partes se realizaban procesos de socialización. Durante el desarrollo de toda la actividad se hacía acompañamiento por parte del docente, para orientar a los estudiantes y animarlos para que pudieran llegar a las soluciones por sus propios medios. Se diseñó una sexta actividad en la cual, a partir de un contexto dado, los estudiantes debían inventar problemas para que sus compañeros los resolvieran y luego ellos mismos debían revisar. Esta actividad tenía como intención que los estudiantes pudieran ver que podían crear matemáticas, decidiendo sobre la validez de los argumentos dados por sus pares.
Para conocer sobre las creencias de los estudiantes se utilizó el cuestionario diseñado y validado por Vizcaíno et al., (2015), contando con el aval de la investigadora principal para su uso. Este cuestionario tiene 18 ítems en total, agrupados en cuatro dimensiones o factores, para cada uno de los cuales se describen las creencias de ingenuas a sofisticadas así:
Factor I: Habilidad innata: En este factor, quienes tienen creencias de tipo ingenuo consideran que la habilidad de la matemática es con algo con lo que se nace y que por tanto unas personas tienen habilidades y otras no; en contraste, quienes tienen creencias sofisticadas creen que si es posible desarrollar las habilidades con el tiempo.
Factor II: Conocimiento simple, dependiente de la autoridad: en la visión ingenua el conocimiento matemático se caracteriza mejor como datos aislados, simples, radicados en una figura externa a ellos; en la sofisticada, el conocimiento es complejo y proviene de diferentes fuentes.
Factor III: Conocimiento relativo-Aprendizaje adquirido: quienes tienen creencias de tipo sofisticado señalan que el éxito para el aprendizaje de las matemáticas está en: el esfuerzo, la dedicación, el estudio sistemático, en indagar y cuestionar; es decir, en tener una actitud propositiva hacia el aprendizaje.
Factor IV: Aprendizaje rápido e inaplicable: la visión ingenua considera que el aprendizaje se da o no se da; en la sofisticada se considera que es lento y gradual.
Para usar este instrumento se contó con el aval de la investigadora principal y se hizo una adaptación al contexto colombiano, a través de la cual se modificaron un par de afirmaciones (León, 2018). El instrumento está diseñado en una escala likert entre 1 y 7 que se asocia con una escala cuantitativa, así: 1. Totalmente en desacuerdo; 2. En desacuerdo; 3. Medianamente en desacuerdo; 4. Ni de acuerdo ni en desacuerdo; 5. Medianamente de acuerdo; 6. De acuerdo; y 7. Totalmente de acuerdo.
Teniendo en cuenta que se trabajó con un solo grupo y que se aplicó el instrumento antes y después de la intervención, se tiene un diseño pre-experimental con preprueba y posprueba en un solo grupo. Las hipótesis planteadas fueron:
Hipótesis de investigación: El diseño y aplicación de actividades con énfasis en resolución de problemas modificará significativamente las creencias que tienen sobre las matemáticas los estudiantes participantes.
Hipótesis nula: El diseño y aplicación de actividades con énfasis en resolución de problemas no modificará significativamente las creencias que tienen sobre las matemáticas los estudiantes participantes.
También se indagó si existían diferencias significativas por género; es decir, si podía cumplirse o no la hipótesis de investigación asociada al género de los participantes. Así mismo, se analizó si existe o no relación de las creencias señaladas y el rendimiento académico y el desempeño de los estudiantes en matemáticas.
El análisis cuantitativo de los datos se llevó a cabo con ayuda del software SPSS, Statistical Package for the Social Sciences. Para probar la existencia de diferencias significativas entre la primera y la segunda aplicación se usó la prueba T-Student. Esta permite contrastar hipótesis a partir del uso de medias en poblaciones con distribución normal.
Para analizar las creencias que tenían los participantes sobre las matemáticas en cada categoría, se determinó el promedio simple, dado en la escala Likert. Debido a que la mayoría de afirmaciones del instrumento al responderlas de manera afirmativa (estar de acuerdo) significaba tener creencias de tipo ingenuo, al calcular el promedio simple, estar cercano a 7, significa creencias de tipo ingenuo; a 1 de tipo sofisticado y no definidas en 4; esto para los factores I, II y IV; para el III la interpretación es al contrario. Por ejemplo, con la afirmación “Algunas personas nacen con grandes habilidades para la matemática y otras no” estar completamente de acuerdo, muestra una visión ingenua frente a las matemáticas. En este sentido, lo que se esperaría con la intervención es que el promedio de los factores I, II y IV disminuya y que el del factor III aumente.
Para determinar si existía correlación entre las creencias y el rendimiento académico después de la intervención, se utilizó la correlación de Pearson. En este caso se analizó la nota final de los estudiantes del curso.
3. Resultados y discusión
En la tabla 2 se muestra el resultado de la prueba T para cada uno de los factores considerados en el instrumento de recolección de información.
Tabla 2 Prueba t para muestras relacionadas en las categorías del Instrumento.
| Diferencias emparejadas | T | gl | Sig. (bilateral) | |||||
|---|---|---|---|---|---|---|---|---|
| Media | Desviación estándar | Media de error estándar | 95% de intervalo de confianza de la diferencia | |||||
| Inferior | Superior | |||||||
| FactorI_Pos- FactorI_Pre | 0,008 | 1,394 | 0,284 | -0,580 | 0,597 | 0,029 | 23 | 0,977 |
| FactorII_Pos- FactorII_Pre | -0,111 | 0,927 | 0,189 | -0,502 | 0,280 | -0,587 | 23 | 0,563 |
| FactorIII_Pos- FactorIII_Pre | 0,198 | 0,964 | 0,197 | -0,209 | 0,605 | 1,006 | 23 | 0,325 |
| FactorIV_Pos- FactorIV_Pre | -0,778 | 1,280 | 0,261 | -1,318 | -0,237 | -2,976 | 23 | 0,007 |
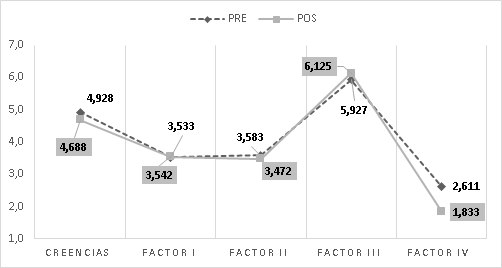
Se evidencia entonces que hubo diferencias significativas solamente en el Factor IV: Aprendizaje rápido e inaplicable, t=-2,976 y p= 0, 007. Esta diferencia evidencia que hubo mejoras luego de la intervención, en relación con las creencias referidas a la velocidad del aprendizaje: en este factor el promedio disminuyó de 2,6 a 1,8, como se muestra en la figura 4.
Las afirmaciones que hacen parte del factor IV son las siguientes: la matemática es como un idioma extranjero para mí, e incluso si trabajo duro, realmente nunca la aprenderé; si no puedo resolver un problema rápidamente, me siento mal y tiendo a darme por vencido; la única razón por la que iría a una clase de matemática se debe a que es obligatorio (Vizcaíno et al., 2015).
Al disminuir el promedio significa que aumenta el nivel de desacuerdo de los estudiantes con estas afirmaciones; es decir, lo que ellos señalan es que al trabajar duro pueden aprender matemáticas, a no darse por vencidos y, además, consideran importante aprender matemáticas. Esto evidencia, como lo señalan McLeod (1988), y Callejo y Vila (2003), que un trabajo en solución de problemas tiene efectos positivos sobre las creencias de los estudiantes. Sin embargo, esto solo ocurrió en tres de los cuatro factores, aunque hubo pequeñas mejoras en los otros tres. Este sin duda es un campo en el que se requiere mucha más investigación.
Para ver si había correlación entre el rendimiento académico o género y las creencias reportadas en cada factor, se utilizó la correlación de Pearson, que se muestra en las tablas 3 y 4. En ellas se evidencia que no hay un nivel de significancia; es decir, que ni el rendimiento académico ni el género tienen relación directa con las creencias reportadas.
Tabla 3 Correlación entre rendimiento académico y creencias por factor.
| Correlaciones | ||||||||
|---|---|---|---|---|---|---|---|---|
| Rendimiento _AC | FactorI_Pos | FactorII_Pos | FactorIII_Pos | FactorIV_Pos | ||||
| Rendimiento_AC | Correlación de Pearson | 1 | -,390 | ,009 | -,068 | -,150 | ||
| Sig. (bilateral) | ,060 | ,968 | ,752 | ,484 | ||||
| N | 24 | 24 | 24 | 24 | 24 | |||
Tabla 4 Correlación entre género y creencias por factor.
| Correlaciones | ||||||
|---|---|---|---|---|---|---|
| Género | FactorI_Pos | FactorII_Pos | FactorIII_Pos | FactorIV_Pos | ||
| Género | Correlación de Pearson | 1 | ,150 | ,216 | ,063 | ,365 |
| Sig. (bilateral) | ,484 | ,310 | ,769 | ,079 | ||
| N | 24 | 24 | 24 | 24 | 24 | |
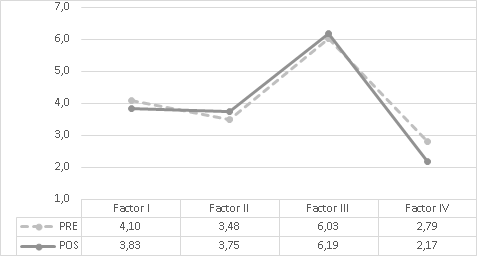
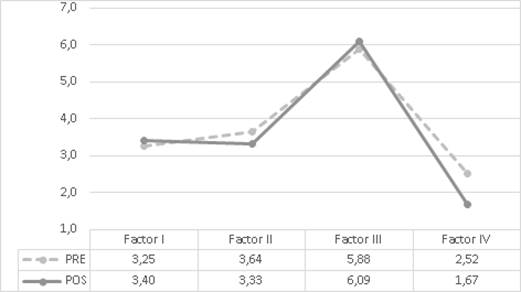
Aunque no hay diferencias significativas por género sí es posible observar, como lo muestran las figuras 5 y 6, que en el factor I después de la implementación, las mujeres se movieron levemente a creencias de tipo sofisticado con respecto al factor I: Habilidad Innata; mientras que los hombres aumentaron creencias de tipo ingenuo. En contraste, en el factor II el comportamiento fue al contrario, las mujeres fortalecieron creencias de tipo ingenuo con respecto a considerar que el conocimiento proviene de una autoridad, y los hombres se movieron hacia creencias sofisticadas. En el factor III, tanto hombres como mujeres se movieron a creencias más sofisticadas, lo mismo ocurrió en el factor IV de manera más importante, ya que fue el único factor que mostró diferencias significativas.
4. Conclusiones
La investigación permitió determinar el efecto que tuvo un trabajo en solución de problemas sobre las creencias matemáticas de un grupo de estudiantes de séptimo grado, en relación con las categorías estudiadas a través del instrumento de Vizcaíno et al (2015). Los resultados permitieron establecer que hubo mejores creencias después de la intervención solamente en uno de los factores, referido a la velocidad del aprendizaje; los estudiantes fortalecieron sus creencias sobre la importancia de esforzarse y no darse por vencido si no se pueden resolver los problemas de manera inmediata. Aunque a partir de los resultados estadísticos no se observaron diferencias significativas en tres de los cuatro factores, ni correlaciones por rendimiento académico o género, durante la intervención sí se pudo observar el gusto de los estudiantes por el tipo de actividades propuestas.
Las mujeres mejoraron sus creencias referidas al factor Habilidad Innata, pues al final de la intervención se movieron hacia creencias más sofisticadas; esto muestra que la intervención sirvió para que se dieran cuenta que no es cierto que se nace con habilidades para las matemáticas y que ese sea un hecho que no se pueda modificar. En cuanto a los hombres, estos se movieron hacia creencias sofisticadas en el factor II, mostrando una visión más compleja sobre el conocimiento matemático. Sin embargo, en estos mismos factores, el género opuesto mostró cambios contrarios, lo cual señala retos investigativos.
Esta experiencia muestra que, para lograr una modificación más significativa sobre las creencias de los estudiantes acerca de las matemáticas, además de ser necesario un trabajo mucho más continuo, es necesario considerar otros aspectos que hacen parte del contexto escolar (Campos, 2008), y tener en cuenta que las creencias primarias son difíciles de transformar y son más estables en el tiempo (Green, 1971) y a su vez afectan creencias derivadas.