INTRODUCCIÓN

La matemática es una de las áreas fundamentales que forma parte del currículo en los primeros años tanto en la escuela como en muchos programas de formación profesional; por ello, una preocupación recurrente en el ámbito de la didáctica está estrechamente ligada con la implementación de estrategias didácticas y de metodologías que optimicen los procesos de enseñanza y de aprendizaje de conceptos matemáticos; por ejemplo, en las últimas décadas la resolución de problemas se ha constituido en una herramienta didáctica muy significativa para el desarrollo de habilidades y de pensamiento matemático entre los estudiantes, puesto que permite al educando enfrentarse a situaciones y problemas que "en teoría como en la práctica" deberá resolver (^{Pérez y Ramírez, 2011}).

Dado lo anterior, la resolución de problemas matemáticos es uno de los aspectos más valiosos de la educación matemática (^{Tzohar y Kramarski, 2014}); desde el siglo XVII René Descartes ya había considerado la existencia de reglas básicas para la resolución de problemas (^{Santos, 1999}), sin embargo, los trabajos en este contexto académico alcanzaron mayor grado de aceptación y refinación a partir de la última mitad del siglo XX, con los postulados de tres importantes teóricos que aún mantienen vigencia en el contexto del aprendizaje de la matemáticas: George Pólya, Alan H. Schoenfeld y Frederick Reif.

Se puede afirmar que, de estos tres, el precursor de la teoría de resolución de problemas matemáticos en el último siglo fue George Pólya, matemático húngaro, destacado por sus aportes en heurística y educación matemática, quien en su trabajo ¿Cómo plantear y resolver problemas?, cuyo título original es How to solve it? (1965), publicado en años de la postguerra, planteó estrategias que contribuyeran no sólo a la solución de problemas matemáticos sino a problemas de la vida cotidiana. Posteriormente, Alan Henry Schoenfeld, investigador y diseñador estadounidense de educación matemática, publicó su libro Mathematical Problem Solving (1985), basado en sus trabajos realizados en los años 80 y refutando algunos de los postulados de la teoría de resolución de problemas de Pólya. Finalmente, Frederick Reif, físico estadounidense, abordó el enfoque de resolución de problemas desde el aprendizaje de la física, ciencia que necesariamente necesita de las matemáticas para existir.

En este artículo de reflexión teórica, además de sintetizar las principales ideas de los autores antes mencionados, teniendo en cuenta sus trabajos o principales obras sobre resolución de problemas, se intenta relacionar cómo cada una de sus propuestas puede reforzar la idea de que al resolver problemas también se promueve de manera implícita o explícita el desarrollo de procesos metacognitivos en el estudiante, específicamente, el desarrollo de regulación metacognitiva, que quisiéramos se dé siempre de manera explícita y permitir "una meditación y análisis más intenso de las operaciones mentales y pensamientos escudriñando una mayor certeza y validez al resolver problemas matemáticos" (^{Bolívar, 2016}, p. 20). En este sentido, se presentará inicialmente, para cada uno de los autores mencionados, las reflexiones sobre los procesos de resolución de problemas y, al finalizar, se expondrá cómo dicho proceso puede estar articulado a la regulación de orden metacognitivo. Lograr esta articulación seguramente ayudará a que tanto docentes como estudiantes desarrollen procesos de enseñanza y aprendizaje de las matemáticas de manera más consciente e intencionada.

RESULTADOS Y DISCUSIÓN

Según ^{Soto (2019)}, "la historia de la resolución de problemas matemáticos puede dividirse en dos grandes etapas delimitadas por la aparición de los trabajos de Polya en 1945" (p. 921). A partir de sus experiencias como matemático y profesor, con la finalidad de bosquejar algunas recomendaciones para docentes y estudiantes de matemáticas (^{Barrera et al., 2021}), George Pólya aportó a la teoría de resolución de problemas matemáticos, principalmente a través de la formulación de varios interrogantes que plantea en su obra How To Solve It? (^{Pólya, 1965}), en la que señala que estas cuestiones son necesarias para estimular el pensamiento de quien confronta el problema, las cuales se sintetizan en 4 etapas:

Es pertinente afirmar, entonces, que los pasos anteriormente mencionados configuran el principal aporte de George Pólya en el aprendizaje de las matemáticas desde el enfoque de resolución de problemas a través de su obra; por medio de la cual el autor inició la formación del profesor de matemáticas posmoderno que requieren las escuelas de hoy, que no sólo enseñe matemáticas de fórmulas y procedimientos, sino que utilice las ciencias exactas para estimular el pensamiento, el ingenio, la creatividad, para lograr la resolución de problemas reales (^{May-Cen, 2015}).

Desde lo planteado hasta este punto, los cuatro momentos o etapas propuestas por Pólya innegablemente se pueden articular a un proceso de pensamiento indispensable en la enseñanza y en el aprendizaje de las matemáticas y de cualquier otra disciplina: la regulación. Referirnos a este proceso es hacer mención, primero, a la metacognición, entendida como el proceso reflexivo que lleva al conocimiento y comprensión de los propios procesos de orden cognitivo que conducen al aprendizaje, más que a la comprensión de lo que se aprende; además, es un mecanismo que brinda al sujeto herramientas para la selección de estrategias y recursos pertinentes para el desarrollo de las tareas propuestas (^{Efklides, 2009}; ^{Núñez et al., 2009}).

Análogamente, en el contexto practico de resolución de problemas, la metacognición, según ^{Brown (1987)}, está asociada a aquellas habilidades ejecutivas que contribuyen a predecir, verificar, monitorear, probar la realidad y coordinar y controlar los intentos deliberados de aprender o resolver problemas, y su uso en el momento y lugar adecuados.

Dentro de la metacognición existe una dimensión macro que puede vincularse a las etapas de Pólya: la regulación (relacionada con el conocimiento, la conciencia del sujeto y las otras dimensiones metacognitivas), la cual desde la actividad de resolver un problema, según ^{Tzohar y Kramarski (2014)}, se refiere a un conjunto de actividades que ayudan a los estudiantes a planificar, monitorear y evaluar su propio trabajo. En esta dimensión, la planeación, el monitoreo y la evaluación son acciones fundamentales, que permiten al sujeto concientizarse del porqué y el para qué de sus acciones y, con ello, seleccionar estrategias pertinentes para enfrentar el propósito de la tarea planteada.

En la planificación (comprensión del problema y concepción del plan, teniendo en cuenta los postulados de Pólya), el estudiante reflexiona sobre el alcance de la tarea, propone estrategias, para él pertinentes, y selecciona, de igual manera, recursos. En el monitoreo y ejecución (ejecución del plan para Pólya) se espera que cada estudiante mantenga la concentración y el interés al aplicar las estrategias y utilizar los recursos seleccionados en la etapa de planeación. En la etapa de evaluación (examinar la solución obtenida para Pólya) no sólo se verifica el logro obtenido, sino también la pertinencia de las estrategias y recursos utilizados y la posibilidad de enfrentar nuevas problemáticas con nuevas estrategias si su balance así lo define.

Así como se identifican similitudes, también es importante exponer puntos que pudieran considerarse adicionar a las etapas propuestas por Pólya y que exhiben oportunidades de enriquecimiento, más que como falencias, para quienes decidan utilizar la perspectiva de Pólya en los ambientes de enseñanza y de aprendizaje de las matemáticas.

Las etapas de resolución de problemas propuestas por Pólya, como se viene ratificando, permiten establecer logros y metas para el problema propuesto, verificar la pertinencia de la estrategia y, muy posiblemente, establecer otras para próximas tareas, sin embargo, podrían enriquecerse con el desarrollo de los procesos metacognitivos y de autorregulación del aprendizaje actual. Primero, establecer junto a los logros y metas del desarrollo del problema, criterios claros y concretos de evaluación de los procesos; segundo, permitir la conciencia y, posiblemente, el control de aspectos de orden motivacional y emocional de los sujetos con el desarrollo de la tarea; y tercero, promover la autoobservación y autocontrol, mediante la expresión de los denominados juicios metacognitivos, que impactarían los procesos de transformación y mejora de los desempeños (^{Zimmerman y Moylan, 2009}).

A partir del fundamento pedagógico de George Pólya, que se puede considerar uno de sus aportes de mayor trascendencia, es pertinente afirmar que este autor abrió camino para las teorías subsiguientes sobre resolución de problemas en el último siglo, ya que otros autores las han construido con base en la obra de Pólya, y si bien es cierto que en este proceso han surgido algunas diferencias conceptuales por parte de otros teóricos, quizás sin las bases cimentadas por Pólya en este contexto, el desarrollo actual de las teorías de resolución de problemas matemáticos no tendría hoy el mismo alcance. En este sentido, uno de esos autores críticos de los planteamientos de Pólya y enriquecedor de la teoría de resolución de problemas es Alan H. Schoenfeld, quien en su obra Mathematical Problem Solving señala cuatro dimensiones para considerar al momento de resolver un problema matemático; Schoenfeld en algunas de ellas refuta elementos planteados por Pólya para resolver un problema matemático.

Las dimensiones consideradas por Schoenfeld son las siguientes:

Adicional a estas dimensiones, otra consideración importante en el trabajo de Schoenfeld es que en el estudio de las matemáticas enfocado en la resolución de problemas, los estudiantes deben reconocer algunos principios epistemológicos, entre los cuales están:

Las dimensiones propuestas por Schoenfeld a partir de su trabajo atinente al enfoque de resolución de problemas matemáticos, también son susceptibles de análisis desde la perspectiva de los procesos metacognitivos que se encuentran inmersos en un problema; en este escenario se pueden discriminar tres procesos en las operaciones de autorregulación de orden jerárquico en la metacognición; esto hace referencia a todas las actividades que el ser humano lleva a cabo de forma autónoma para controlar todo lo que realiza y aprende; estos procesos son: planeación, monitoreo y evaluación.

Primeramente es necesario tener en cuenta que los procesos metacognitivos son los que sistematizan las labores cognitivas, las cuales en un evento de resolución de problemas, por ejemplo, si la persona concibe, examina o monitorea mientras soluciona el problema, es factible que logre adicionar los procesos metacognitivos a esta solución, ya que son un elemento fundamental del componente afectivo; forjando de las creencias de cada individuo posibles principios predominantes de sus pensamientos y actitudes, tal como lo testifica ^{Schoenfeld (1992)} en el momento de resolver problemas matemáticos (^{Bolívar, 2016}).

Teniendo en cuenta lo anterior, y que la regulación metacognitiva se refiere al conjunto de actividades que ayudan al estudiante a controlar su aprendizaje (Tamayo, 2006), es pertinente afirmar que los procesos metacognitivos permiten a los estudiantes ser conscientes de qué técnicas o estrategias son más útiles al momento de resolver un problema; de esta forma, la planeación corresponde a las disposiciones y estrategias que se llevan a cabo para poder resolver el problema, es decir, búsqueda de estrategias para cumplir con la resolución del problema, una vez identifica la situación vinculada con este (López, 1992, citado por ^{Bolívar, 2016}). Es válido considerar, entonces, que dentro de un proceso de planeación se considere, en primer lugar, los recursos que se tienen para resolver un problema, siendo precisamente los recursos la primera dimensión que plantea Schoenfeld. Según ^{Santos (1999)}, en esta primera fase de acercamiento hacia el problema es importante reflexionar en cuestiones tales como "qué se pide", "qué se tiene" y "a donde se quiere llegar". En segundo lugar, según ^{Schoenfeld (1992)}, citado por ^{De Jesús (2020)}, se deben considerar como factores que intervienen en el proceso de resolución de problemas: las estrategias cognitivas o heurísticas, que involucran formas de representar y explorar los problemas con la intención de comprender los enunciados y plantear caminos de solución; las estrategias metacognitivas, que involucran conocimiento acerca del funcionamiento cognitivo propio del individuo (¿Qqé necesito?, ¿cómo utilizo ese conocimiento?), y estrategias de monitoreo y control del propio proceso cognitivo (¿qué estoy haciendo?, ¿por qué lo hago?, ¿a dónde voy?).

Respecto a los procesos de Monitoreo y evaluación, se pueden asociar con la dimensión de control, en la cual la persona que está resolviendo el problema debe contar con la habilidad para monitorear y evaluar el proceso. Respecto a esta dimensión, Schoenfeld señala que es, también, conocimiento de sí mismo: la persona que está resolviendo el problema debe saber qué es capaz de hacer, con qué cuenta, o sea, conocerse en cuanto a la forma de reaccionar ante esas situaciones (^{Carreño et al., 2017}).

El mismo Schoenfeld en sus trabajos prácticos atinentes a su enfoque sobre resolución de problemas matemáticos "incluyó un conjunto de estrategias de monitoreo. (...) Estas contienen preguntas en las cuales los estudiantes tienen que evaluar las decisiones tomadas en el proceso de resolver problemas" (^{Santos, 1999}, p. 21). Además de los anterior, según ^{Santos (1999)}, en los trabajos de Schoenfeld, este plantea que "estrategias metacognitivas se relacionan con el monitoreo empleado al resolver el problema, por ejemplo, el proceso de selección de una estrategia y la necesidad de cambiar de dirección como resultado de una evaluación permanente del proceso" (p. 22).

Finalmente, la evaluación, realizada al final de la tarea, se refiere a la naturaleza de las acciones y decisiones tomadas por el aprendiz; evalúa los resultados de las estrategias seguidas en términos de eficacia (^{De Jesús, 2020}). Respecto a este proceso, algunos autores distinguen y diferencian las estrategias de evaluación de las demás estrategias cognitivas y las consideran como estrategias metacognitivas que controlan la eficiencia de las acciones cognitivas en los procesos de resolución de problemas (^{Rocha-Silva, 2006}).

Ahora, sobre la dimensión: sistema de creencias de Schoenfeld, no la ubicamos de manera específica en una de las tres etapas de regulación metacognitiva. La razón que nos lleva a este planteamiento es que "las creencias establecen el contexto en el cual los recursos matemáticos y metacognitivos y las heurísticas operarán" (^{Hidalgo et al., 2015}, p. 69); en otras palabras, las creencias condicionan el porqué y el para qué del uso de los recursos y de las heurísticas que el sujeto identifica como necesarias para la resolución del problema. En el campo metacognitivo, las creencias podrían llamarse conocimiento estratégico del individuo, una dimensión que sobrepasa la regulación metacognitiva y se ubica en la dimensión de la conciencia metacognitiva, pues requiere, además del dominio de estrategias y procedimientos, su uso intencional y consciente articulado a las metas y demandas de la tarea (^{Pozo, Monereo y Castelló, 2001}).

El tercer autor que decidimos poner en contraste para los procesos de resolución de problemas es Frederick Reif, quien en sus trabajos sobre este tema describe un estudio sistemático de habilidades para resolver problemas en física básica. También analiza cómo se utilizan observaciones detalladas de individuos para formular modelos para los procesos de resolución de problemas en mecánica y aplicaciones para la enseñanza universitaria básica de física o cursos de ingeniería.

Reif (2008) en su libro "Applying Cognitive Science to Education - Thinking and learning and other Complex Domain" manifiesta que resolver un problema puede ser difícil y requiere de la toma cuidadosa de decisiones; por ello propone una estrategia ventajosa para la solución de problemas basada en dos reglas generales que facilitan resolver tareas más complejas. La primera regla consiste en "divide y vencerás", es decir, cualquier tarea compleja se puede realizar más fácilmente si se descompone en partes más sencillas de manejar o de manipular; más exactamente, es muy útil descomponer un problema en subproblemas, entendido un subproblema como aquel cuya solución aporta a la solución del problema original; este proceso de descomposición se puede llevar a cabo de manera iterada hasta donde se considere pertinente. La segunda regla denominada, "aproximaciones sucesivas", plantea que a menudo es difícil lograr una meta como resultado de un solo esfuerzo mayor. En cambio, un problema puede abordarse más gradualmente mediante un proceso de aproximaciones sucesivas, en el que cada aproximación obtenida se acerca gradualmente a la solución deseada.

Las dos anteriores reglas son fusionadas en la siguiente estrategia básica, que consta de cinco pasos, para solución de problemas:

Además de esto, según ^{Guisasola et al. (2007)} para facilitar la resolución de problemas desde la perspectiva de Reif, se consideran de gran interés los siguientes factores: una organización jerárquica del conocimiento que facilite la elección de la vía de resolución y la adquisición previa de una serie de habilidades de interpretación y representación del conocimiento.

De forma similar a las comparaciones establecidas entre las ideas de Pólya y Schoenfeld en cuanto a la resolución de problemas frente a los procesos de orden metacognitivos, los planteamientos de Reif también se pueden vincular a los procesos de planeación, monitoreo y evaluación, comparación que se sintetiza en la tabla 1.

Tabla 1 Pasos para solución de problemas según Reif vs. Procesos metacognitivos 

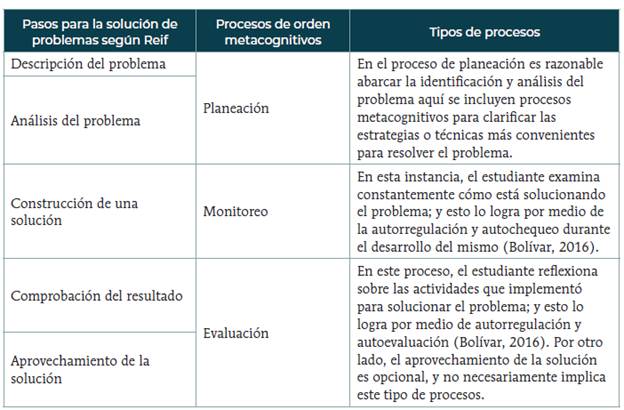
Nota: esta tabla muestra los pasos para solución de problemas según Frederick Reif, teniendo en cuenta procesos de orden metacognitivos.

Al igual que Schoenfeld, Reif va más allá de los procesos de regulación metacognitiva en su fase "aprovechamiento de la solución"; esto porque, además de aportar al desarrollo de acciones conscientes al resolver un problema, también promueve, para nuevas situaciones, el uso consciente e intencionado de los procedimientos utilizados, desde la evaluación de la eficacia y eficiencia que tuvo al resolver la tarea.

Al comparar las teorías, postulados, dimensiones o componentes referidas a la resolución de problemas, planteados por George Pólya, Alan H. Schoenfeld y Frederick Reif, se debe considerar primeramente que el trabajo de Pólya en este ámbito influenció en gran medida todos los modelos de resolución de problemas que se publicaron posteriormente, entre ellos el de Schoenfeld, que si bien es cierto que basó parte de sus teorías en el libro de Pólya "How to solve it", tomó distancia de algunos aspectos pertinentes a los métodos heurísticos planteados en esta obra, al considerar que sus alcances son limitados.

George Pólya planteó cuatro etapas para la resolución de un problema: comprender el problema, concebir un plan, ejecución del plan y examinar la solución obtenida. Aunque estas etapas han sido asumidas por distintos modelos de resolución de problemas planteados por otros autores, sólo convergen, desde un punto de vista formal, en el sentido que señalan, esencialmente, consideraciones básicas y comunes a todos ellos (^{Ceberio et al., 2008}).

Por su parte, Alan H. Schoenfeld discriminó cuatro dimensiones: Recursos, Heurísticas, Control y Sistema de creencias; aunque también concluyó que en el trabajo de resolución de problemas hay que tener en cuenta situaciones más allá de las puras heurísticas; de lo contrario no funciona, no tanto porque las heurísticas no sirvan, sino porque hay que tomar en cuenta otros factores (^{Barrantes, 2006}); siendo este aspecto el que marca diferencias fundamentales entre la teoría de este autor frente a los postulados de Pólya. De forma general, según ^{Santos (1999)}, el trabajo de Schoenfeld ,visto desde el enfoque de resolución de problemas, incorpora un punto de vista de las matemáticas en la cual los estudiantes son motivados a discutir el sentido de las ideas matemáticas.

Mientras que Frederick Reif aborda la resolución de problemas desde el contexto de la física a través de dos reglas generales, fusionadas en una estrategia de cinco fases: descripción, análisis inicial del problema, construcción de una solución, comprobación del resultado y aprovechamiento del mismo. Lo anterior considerando además factores pertinentes a la organización del conocimiento y a la adquisición de habilidades de interpretación y representación del conocimiento.

Aunque los aportes de Reif en el enfoque de la resolución de problemas gozan de gran aceptación en las ciencias básicas, su aplicabilidad tiende a ser mayor en el aprendizaje de la física más que en las matemáticas; además, sus teorías en este contexto han sido menos documentadas que las de Pólya y Schoenfeld, por lo menos en investigaciones en habla hispana.

Un elemento de gran importancia para tener en cuenta en las teorías de resolución de problemas de los tres autores mencionados son los procesos de orden metacognitivos, de los cuales se asume que la regulación metacognitiva mejora el rendimiento en diferentes formas: mejora el uso de la atención, proporciona una mayor conciencia de las dificultades en la comprensión y mejora las estrategias ya existentes; respecto a esto se ha encontrado un incremento significativo del aprendizaje cuando se incluyen como parte de la enseñanza, la regulación y la comprensión de las actividades (^{De Jesús, 2020}).

Teniendo en cuenta lo anterior, es de destacar que los procesos de planeación, monitoreo y evaluación están vinculados de manera concreta con las etapas de Pólya, Schoenfeld y Reif; sin embargo, los dos últimos logran trascender la dimensión de la regulación metacognitiva y proponer (implícita o explícitamente) una articulación con la dimensión de la conciencia y conocimiento del sujeto, indispensable para hacer más eficiente los desempeños.

Sin embargo, cabe resaltar que según ^{Garofalo y Lester (1985)}, aunque los procesos de orden metacognitivos revisten considerable importancia y se asumen en varios modelos de resolución de problemas desde los mismos postulados de Pólya, los educadores matemáticos no los han estudiado sistemáticamente; esta falta de atención a la metacognición se atribuye a las siguientes razones:

Lo antes mencionado tiene que ver también con el hecho de que aunque existen diferentes métodos de resolución de problemas matemáticos como los descritos anteriormente, los estudiantes generalmente tienen dificultades al resolver problemas de mayores niveles de dificultad, ya que esos problemas no solo exigen el dominio de habilidades matemáticas básicas, sino que también requieren procesos cognitivos superiores o metacognición como transformaciones o una serie de formulación y reformulaciones para resolverlos (^{Duncker, 1945}).

En esto coinciden diferentes autores, quienes afirman que además de la capacitación en estrategias y tácticas de resolución de problemas, los estudiantes necesitan capacitación en direcciona-miento y control, así como también en autorregulación y desarrollo mental (^{Desoete et al., 2003}; ^{Ginsburg y Fantuzzo, 1998}; ^{Pape y Smith, 2002}).

CONCLUSIONES

De acuerdo con los resultados de este artículo y de su discusión, de la comparación con resultados de otros autores y del detallado análisis presentado, se pueden extraer las siguientes tres conclusiones principales: